Probability & Statistics

YOU ARE LEARNING:

Probability Tree Diagrams and Independent Events 2

We can have more than two outcomes for each event, and we can build this into our probability tree diagram.

Tree diagrams are a great way to display all the possible outcomes for a given event. We can use them to describe more complicated events where there are three possible outcomes at each event.

To find the probability of two events both happening, which calculation is correct?

Let's have a look at a situation where there are three possible outcomes, with $3$ branches in the tree diagram.

In this example, there are 3 possible outcomes at each step

There are 2 red balls, 3 yellow balls and 1 green ball in a bag. Oliver removes one ball from the bag, notes the colour and replaces it. He then removes another ball.

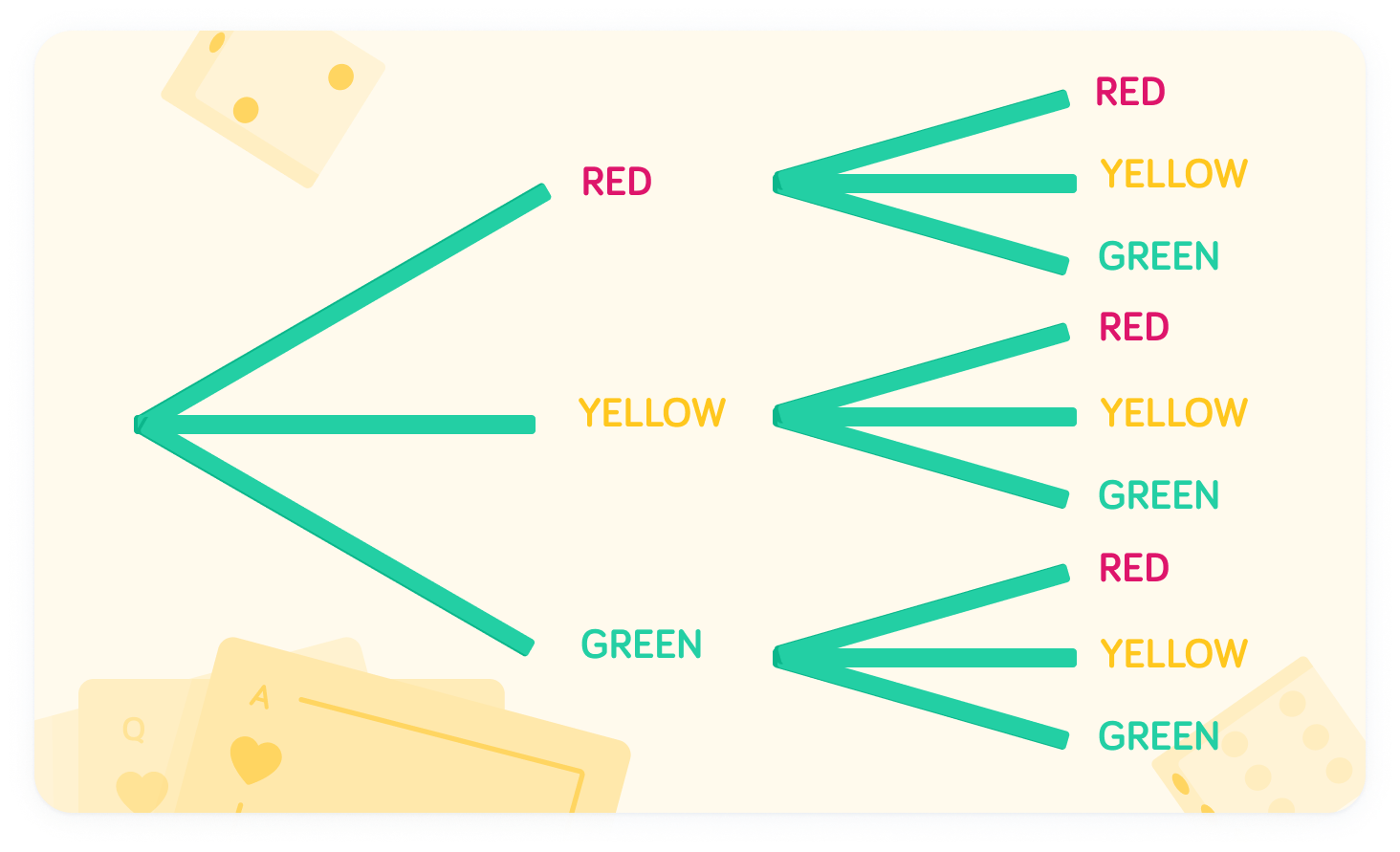
We can plot this on a tree diagram

When Oliver removes a ball from the bag, there are three options - red, green or yellow. This can be displayed as three “branches”. Since the ball is replaced, this is repeated for the second ball.

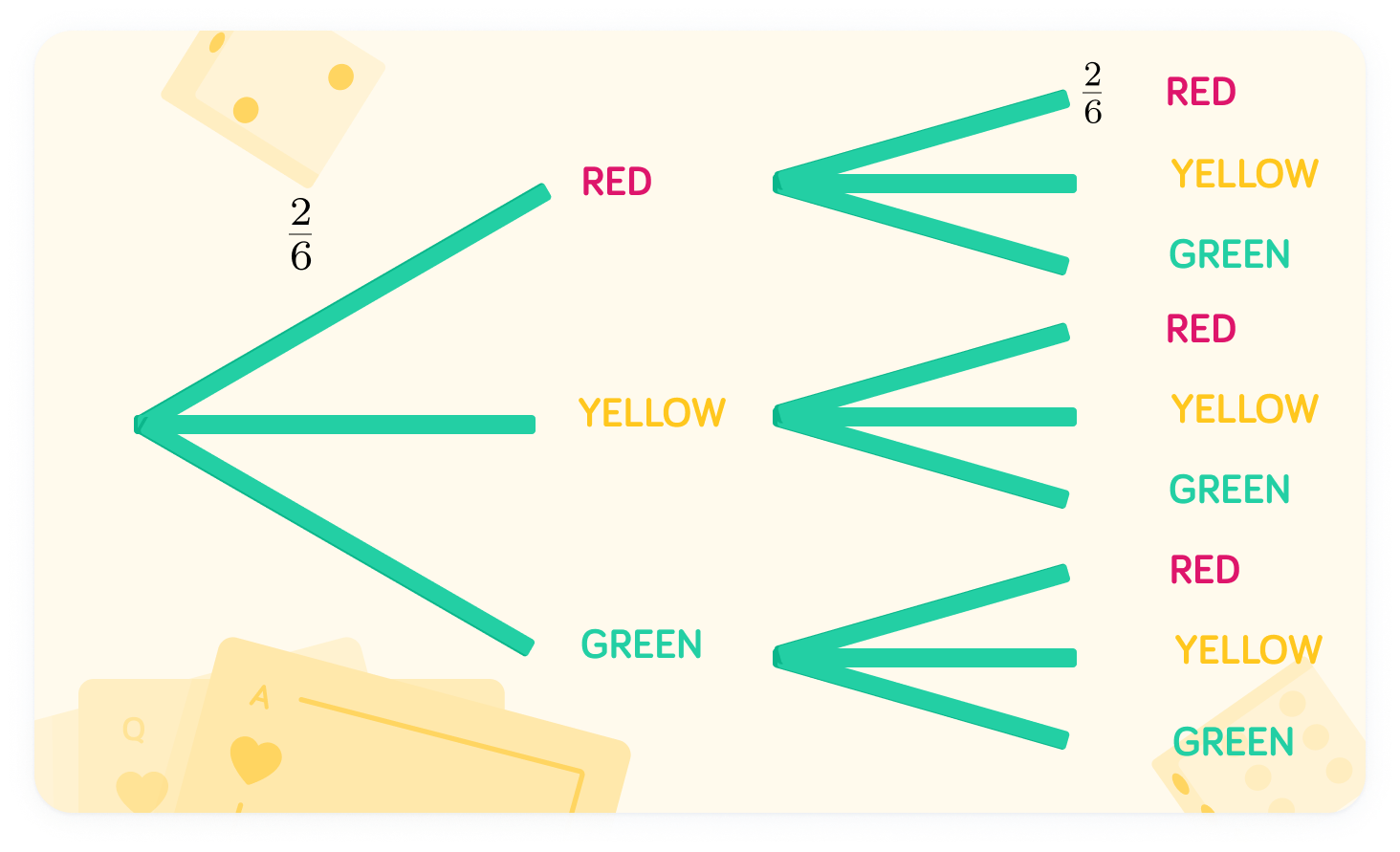
There are 3 yellow balls. What should we write upon the yellow branches?

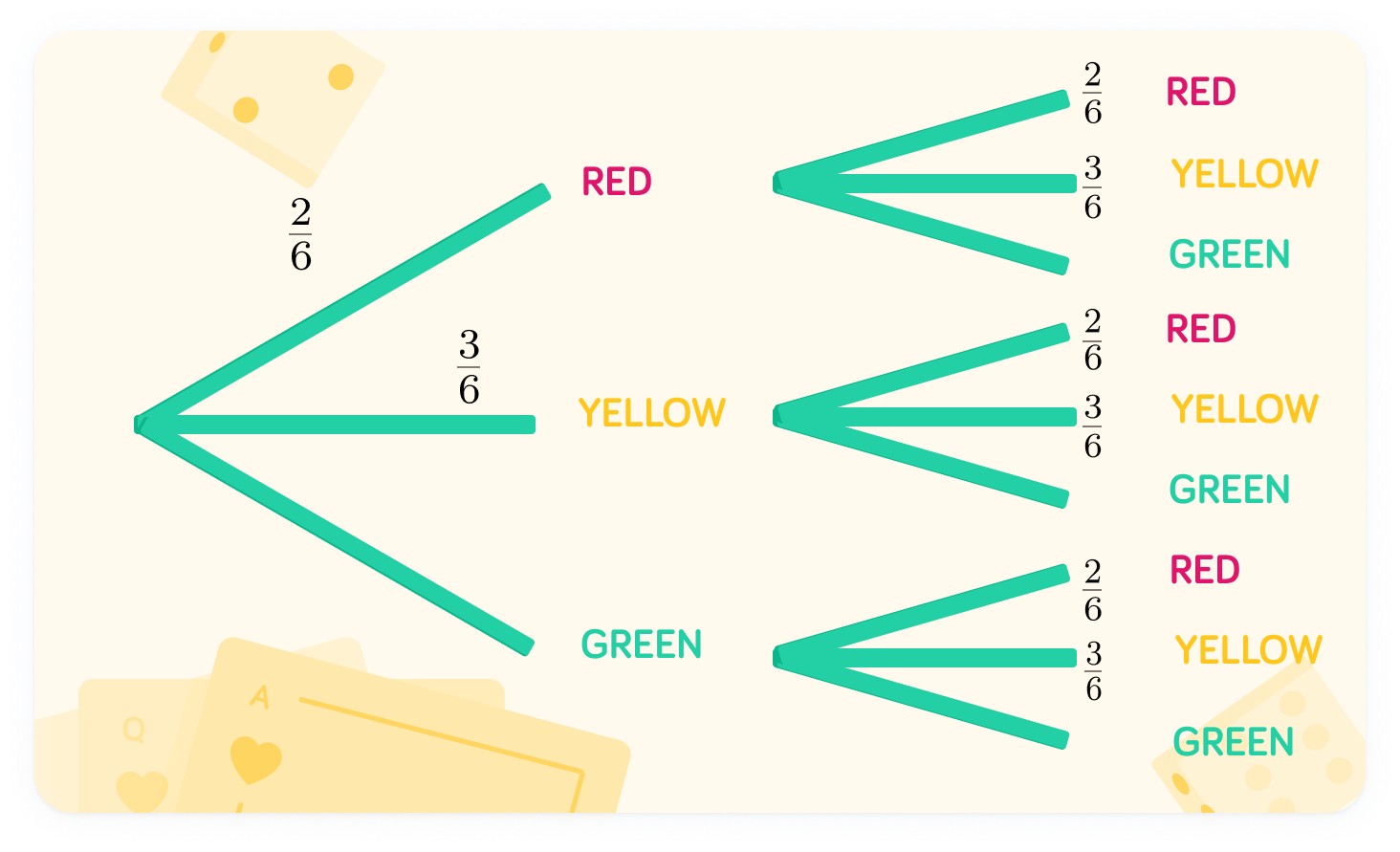
What should we write upon the green branches?

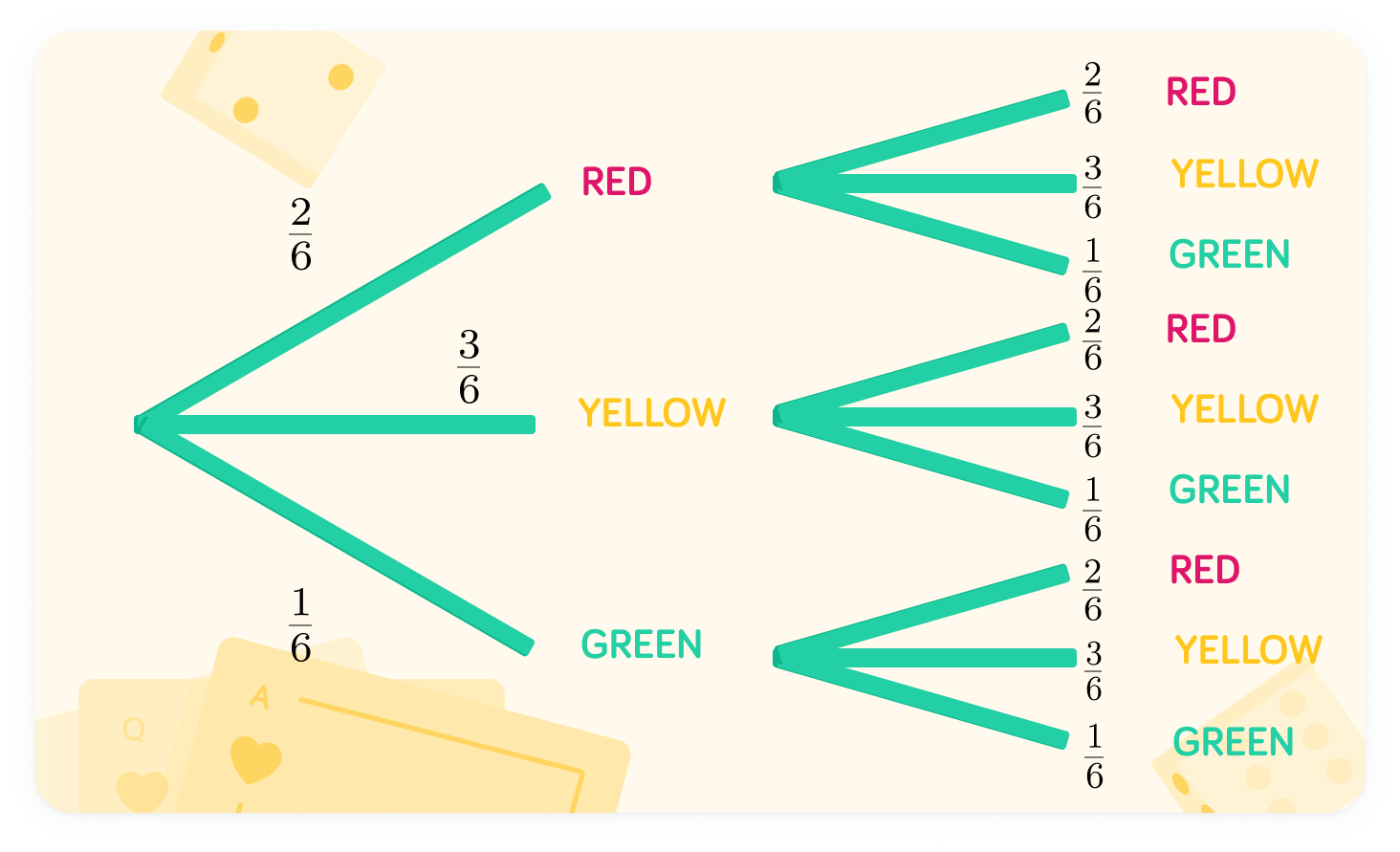
This is the completed tree diagram

Though there are 3 branches in each case, the rules are the same, and we can use the diagram to find out information about the combined probabilities of multiple events.

The probability of hitting a target is $0.6$ , and the probability of missing is $0.4$ . What is the probability of hitting the target twice in a row?

When events are mutually exclusive, we can find the probability of either one event, or another, happening. This is called the or rule of probability, and requires us to add the probabilities together.

For example, when rolling a die, the probability of rolling either a 5 or a 6 adds the probability of each individual event together. This is because the probability of either event is greater than the probability of only one of the events happening.

Have a look at the completed tree diagram

It shows the probabilities of choosing one of three coloured balls across two picking events.

Let's work out the probability of picking two balls of the same colour

There are multiple ways to achieve this, since there are three colours. The opportunities are red/red, yellow/yellow, and green/green. Since these events can't happen at the same time, we need to add the probabilities together.

What is the probability of picking two green balls?

The probability of two green balls is $\dfrac{1}{36}$

To find this, we need to multiply the probabilities together: $\dfrac{1}{6} \times \dfrac{1}{6}=\dfrac{1}{36}$

What is the probability of picking two yellow balls?

The probability of two greens is $\dfrac{9}{36}$

By multiplying the probabilities of green together, we find $\dfrac{3}{6} \times \dfrac{3}{36} = \dfrac{9}{36}$

What is the probability of picking two red balls?

The probability of two red balls is $\dfrac{4}{36}$

We can calculate this by multiplying the probabilities: $\dfrac{2}{6} \times \dfrac{2}{6} = \dfrac{4}{36}$

To find the probability of any one of these events happening, add the probabilities

Now we know the probability of each method of picking the same coloured ball, we can add them together. Our calculation should therefore be $\dfrac{1}{36} + \dfrac{4}{36} + \dfrac{9}{36}$

What is $\dfrac{1}{36} + \dfrac{4}{36} + \dfrac{9}{36}$ ?

The probability of picking the same colour is $\dfrac{14}{36}$

$\dfrac{1+4+9}{36}=\dfrac{14}{36}$

What is the simplest version of $\dfrac{14}{36}$ ?

Nice! The simplified fraction is $\dfrac{7}{18}$

This is the final answer - the probability of picking two balls of the same colour is $\dfrac{7}{18}$