Atoms and Radioactivity

YOU ARE LEARNING:

Half-Life Curves: Background Radiation Included

To find the half-life of a sample, we must subtract the background radiation from our measurements.

What is the half-life of this particle sample?

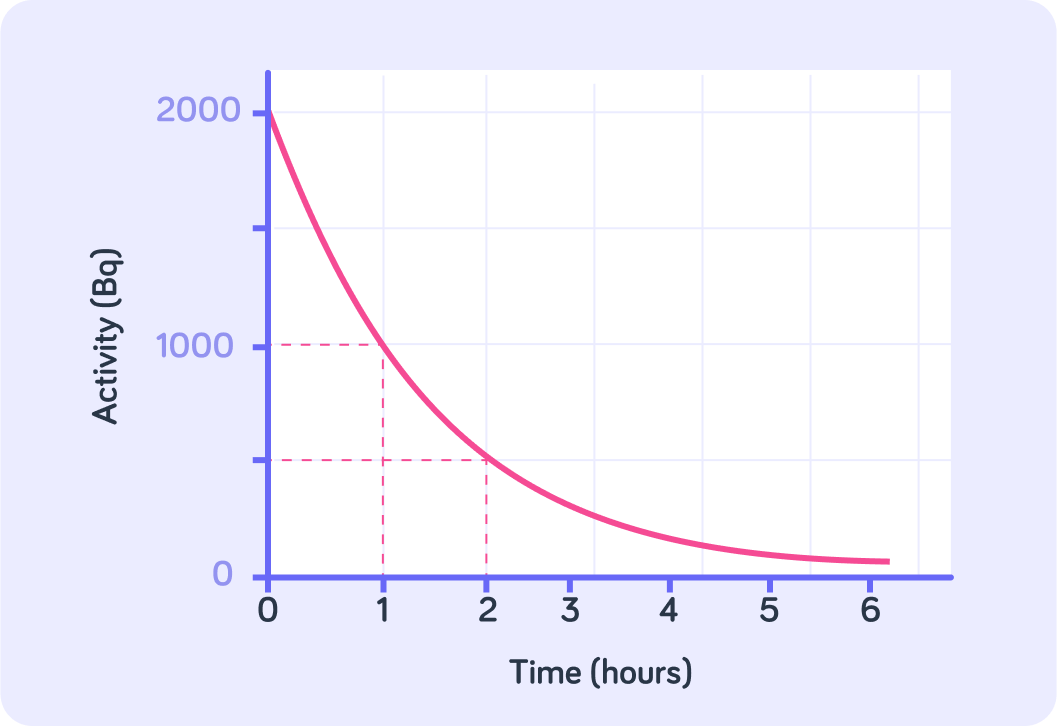
As more and more time goes by, what value does the activity tend toward?

The activity in a sample will get closer to zero as more and more time goes by.

This is because as more and more unstable isotopes decay, there will be fewer and fewer unstable isotopes in the sample. Eventually, there will be none left to decay.

Now, what is background radiation?

There are a few things we need to think about when we measure the activity of a radioactive substance.

First of all, when we measure the count rate with a Geiger-Muller tube and counter for example, we don't actually measure all of the radiation it emits every second. Why do you think that is?

So with a Geiger-Muller tube and counter, we actually only measure a fraction of the activity of the sample.

If we were to measure all the activity, we would have to somehow create a detector that could surround the entire sample.

Secondly, when we use a detector like Geiger-Muller tube and counter, we also inevitably measure something we are not really interested in measuring. What?

So when we measure the activity in a sample of a radioactive substance there are two things to remember

We are not measuring all the activity in the sample, and whatever value we measure also includes background radiation. The detector doesn't separate the activity of the sample from the background radiation.

This graph shows the count rate of a radioactive sample

It has been measured with a detector, for example a Geiger-Muller tube.

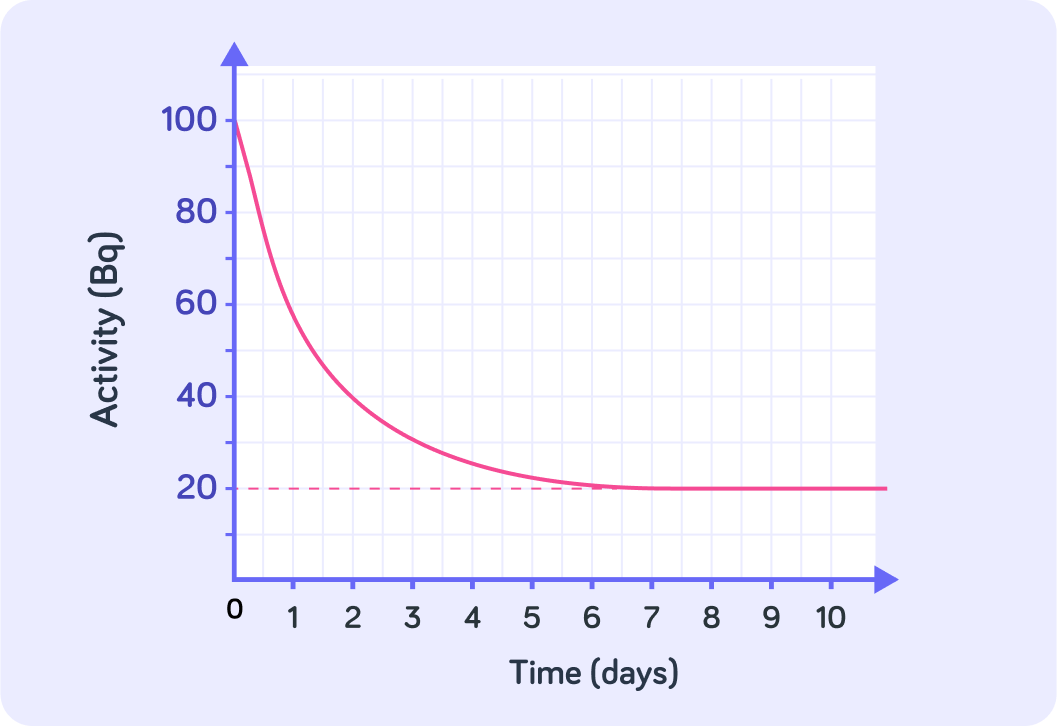
True or false? The curve in this graph does not tend toward zero.

So the activity for this sample never seems to reach zero. This is because the detector also picks up the activity of ____________ ____________.

What is the activity of the background radiation here?

So rather than tending toward zero, the curves tends towards 20 Bq

That means that the activity of the background radiation here must be 20 Bq.

In order to measure the half-life, we must take into account this background radiation.

This means we have to basically pretend that 20 Bq is 0 Bq on this graph.

If the detector counts 100 Bq activity from both the sample and background radiation combined, then what is the activity in Bq that comes only from the sample?

Now, if we want to find the half-life for this sample from looking at the graph, at which Bq value on the y-axis should we start?

So we read off the half-life of this sample from the value 60 Bq on the y-axis. What is this sample's half-life then?

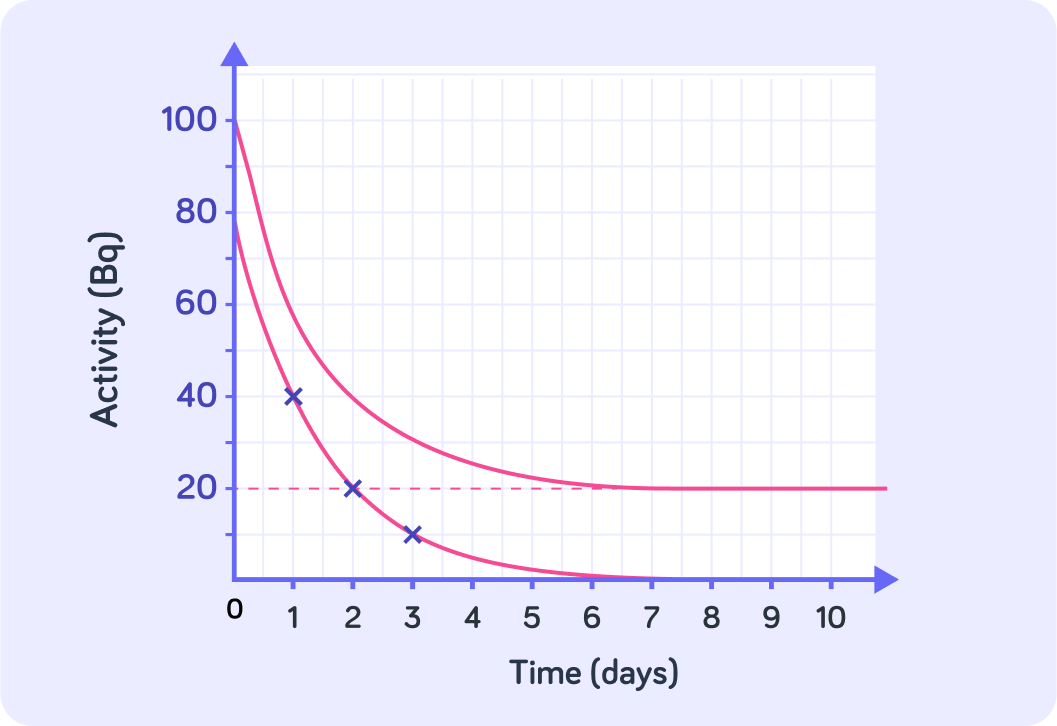
We can also calculate the correct half-life by re-drawing the curve, so that it does tend toward zero

Choose easy points and subtract 20 Bq from them and draw them on the graph. Then connect the dots to find the correct curve that does not include the background radiation.

Summary!

When you measure the activity of a radioactive sample, the detector also includes background radiation

You have to make sure that you account for this background radiation when you decide the half-life of this sample.

You will be able to see what the background radiation is from plotting the activity on a graph.

With background radiation, the graph will not tend toward zero. It will flatten out at the value of the background radiation activity.

You can then subtract the value of the background radiation activity from the total value you measured

That way you can find the real activity of the sample and its half-life.