Atoms and Radioactivity

YOU ARE LEARNING:

Net Decline

The net decline is how much the the count rate of a sample has decreased by after radioactive decay.

Detectors such as a Geiger-Muller counter and tube measure the count rate of a radioactive sample. What is the count rate really?

A) The activity of the sample B) The number of particles or rays detected per second C) The half-life of the sample

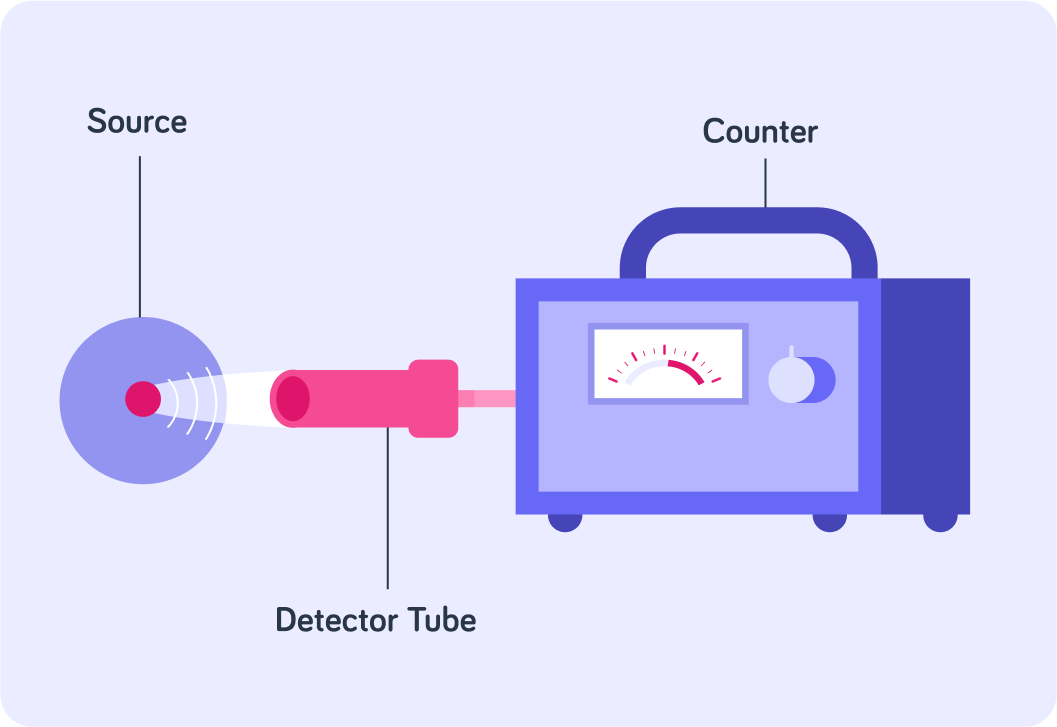
When we measure the count rate of a sample, we usually only measure a fraction of the radiation that gets emitted by the sample.

If we wanted to measure all the activity in the sample, we would have to use a detector that would somehow surround the entire source.

True or false? When we measure the activity of a radioactive sample with a detector, we get an exact value for the activity of the sample.

The activity we measure, for example with a Geiger-Muller tube and counter, will only be an estimate of the entire sample's activity.

This is because the detector doesn't count all the radiation that gets emitted by the sample. It only counts a fraction.

Radioactive decay causes the number of unstable nuclei in a sample to decrease. What does this mean for the count rate measured by a detector, like as a Geiger-Muller counter and tube?

How do we define the half-life for a radioactive sample?

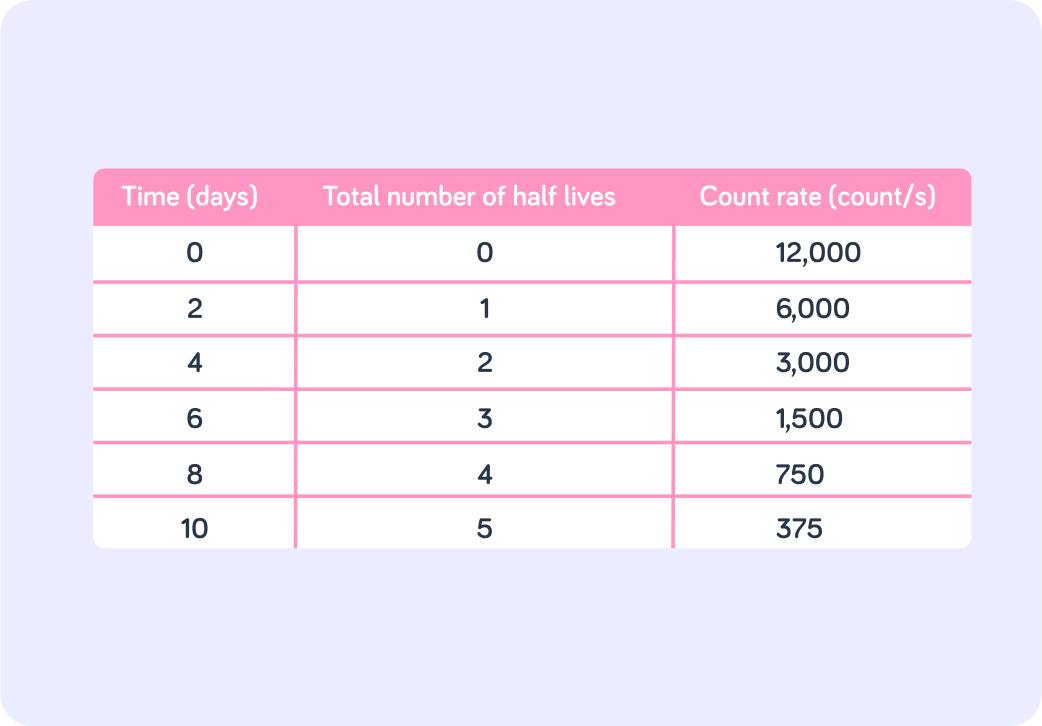
This table shows how the count rate of a particular radioactive sample changes over time. What is the half-life of this sample?

How much does the count rate fall by after each half-life?

A) 25% B) 50% C) 100%

Now, say you want to find out how much the count rate has decreased over 4 half-lives in percent.

To do that, you need to know the initial count rate and the count rate after 4 half-lives.

What is the initial count rate?

What is the count rate after 4 half-lives?

So after 4 half-lives there are $750 \space counts/s$ left out of $12,000 \space counts /s$ . How would you write that as a fraction?

Now simplify $\frac{750}{12,000}$ as much as possible. What fraction do you get?

So after 4 half-lives there is only one 16th left of the initial count rate.

This is the same as multiplying $\frac{1}{2}$ by itself 4 times: $\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{16}$

What is $\frac{1}{16}$ as a percentage?

So after 4 half-lives the count rate in the sample has decreased to $6.25\%$ of the initial count rate.

$\frac{750 \space counts/s}{12,000 \space counts/s} = \frac{1}{16} = 0.0625 = 6.25\%$

What percentage of the initial number of isotopes are left after 3 half-lives in this sample? Give your answer as a percentage.

What percentage of the initial number of isotopes are left after 5 half-lives in this sample? Give your answer as a percentage.

Do you see the pattern?

After 1 half-life: $\frac{1}{2}=50\%$ remains After 2 half-lives: $\frac{1}{4}=25\%$ remains After 3 half-lives: $\frac{1}{8}=12.5\%$ remains After 4 half-lives: $\frac{1}{16}=6.25\%$ remains After 5 half-lives: $\frac{1}{32}=3.13\%$ remains

Which one of these is the formula you have been using to calculate the percentage of isotopes left after a certain amount of half-lives?

True or false? The count rate of a radioactive sample after 3 half-lives will be $\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8}$ of the initial count rate.

Now, net decline is not the percentage of isotopes that is left after a certain number of half-lives. It is the amount that the number of isotopes (count rate) have decreased by in percentage.

This is similar to calculating how a sale reduces prices. Say a T-shirt is initially £100 but the sale reduces that to £90. How much has the price decreased by?

Similarly, the original number of nuclei is 100%. If the final number of nuclei left as a percentage is 95%, what is the percentage decrease?

What is the net decline after 2 half-lives if your sample has gone from $12,000 \space counts/s$ to $3,000 \space counts/s$ ? Give your answer as a percentage.

So to calculate the net decline, you have to subtract the count rate after X half-lives from the initial count rate before you find the percentage: $net \space decline = \frac{(initial \space count \space rate)-(count \space rate \space after \space X \space half \space lives)}{initial \space count \space rate}\times 100$

For example: $net \space decline = \frac{(12,000 \space counts/s)-(3,000 \space counts/s)}{12,000 \space counts/s}\times 100 = 75\%$

Summary

We can calculate how big a fraction and percentage is left of the initial amount of isotopes in a radioactive sample after a certain amount of half-lives

We can translate these fractions into percentages

$\% \space isotopes \space left = \frac{count \space rate \space after \space X \space half \space lives}{initial \space count \space rate}\times 100$

Net decline is how much the amount of isotopes (count rate) has decreased by.

It is not simply how big the fraction of isotopes that remains is!

We can calculate net decline this this

$net \space decline = \frac{(initial \space count \space rate)-(count \space rate \space after \space X \space half \space lives)}{initial \space count \space rate}\times 100$

So if the fraction of isotopes that remains is $\frac{1}{4}$ or $25\%$ after 2 half-lives...

then net decline is $75\%$