Graphs

YOU ARE LEARNING:

Cubic Graphs

Cubic graphs are curved graphs, where the highest power of x is 3. A table of values can be used to work out each point on the graph.

Cubic graphs are functions where the highest power of $x$ is $x^3$ . They can have a variety of shapes depending on the specific function being displayed.

Let's draw the graph of $y = x^3 -2x^2 -5x$

For each $x$ coordinate, we can find the corresponding $y$ coordinate by ....

.... substituting the $x$ value into the equation.

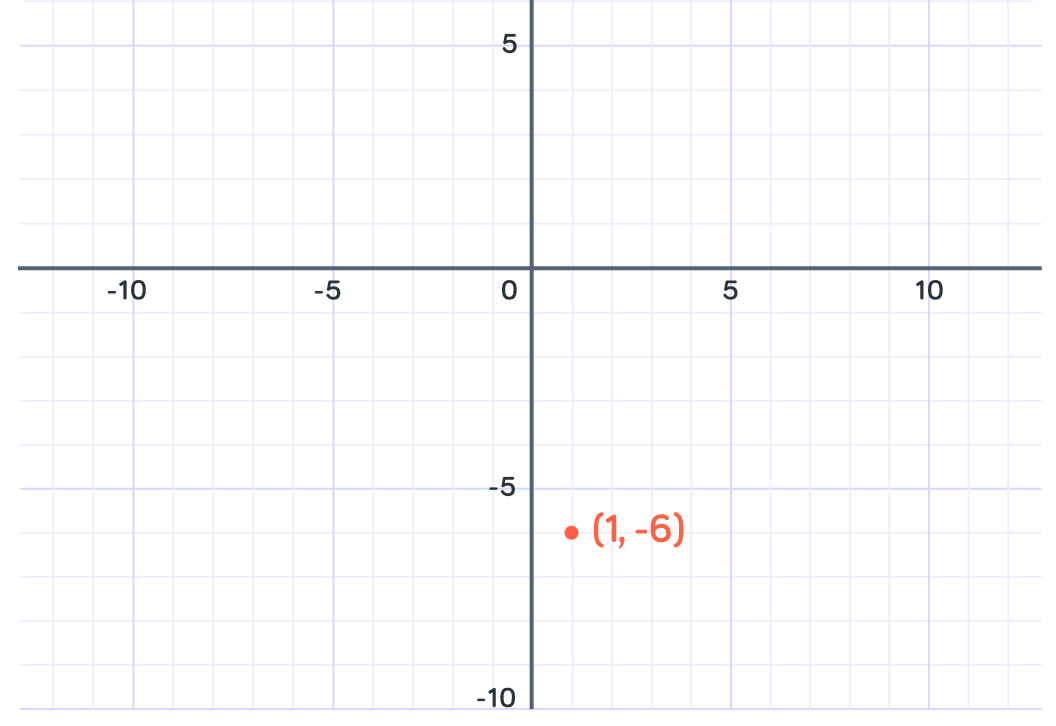
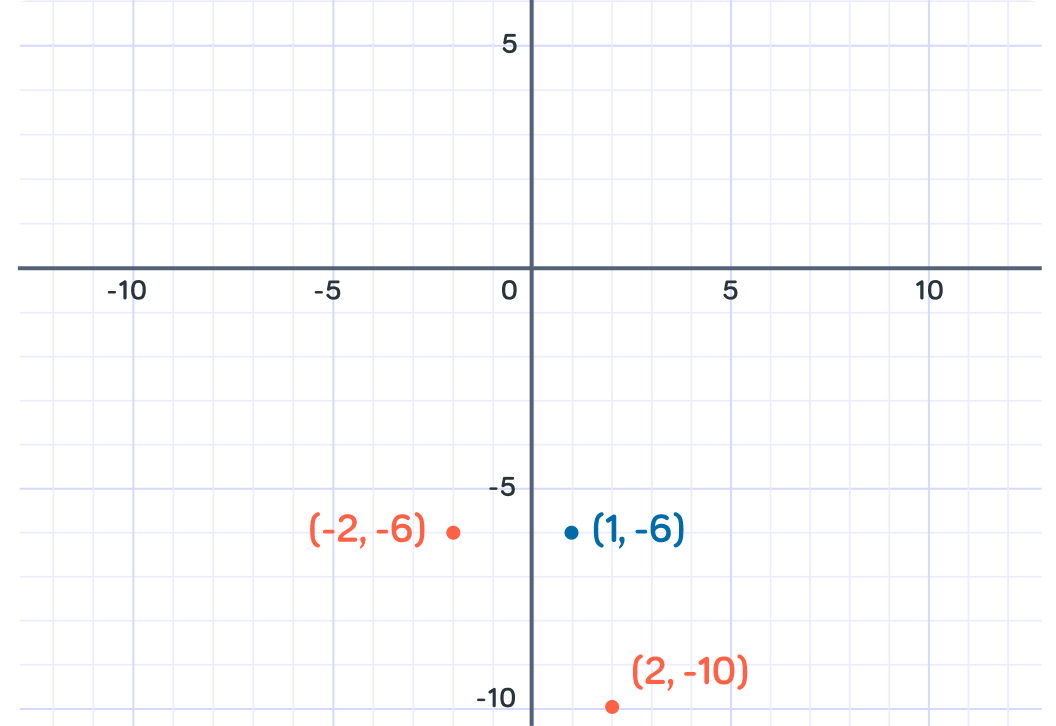
For example, when $x=1$ , $y=-6$

$y=1^3-(2 \times 1^2)-(5 \times 1)$ so $y=-6$ . We can plot this point on the graph at $(1,-6)$

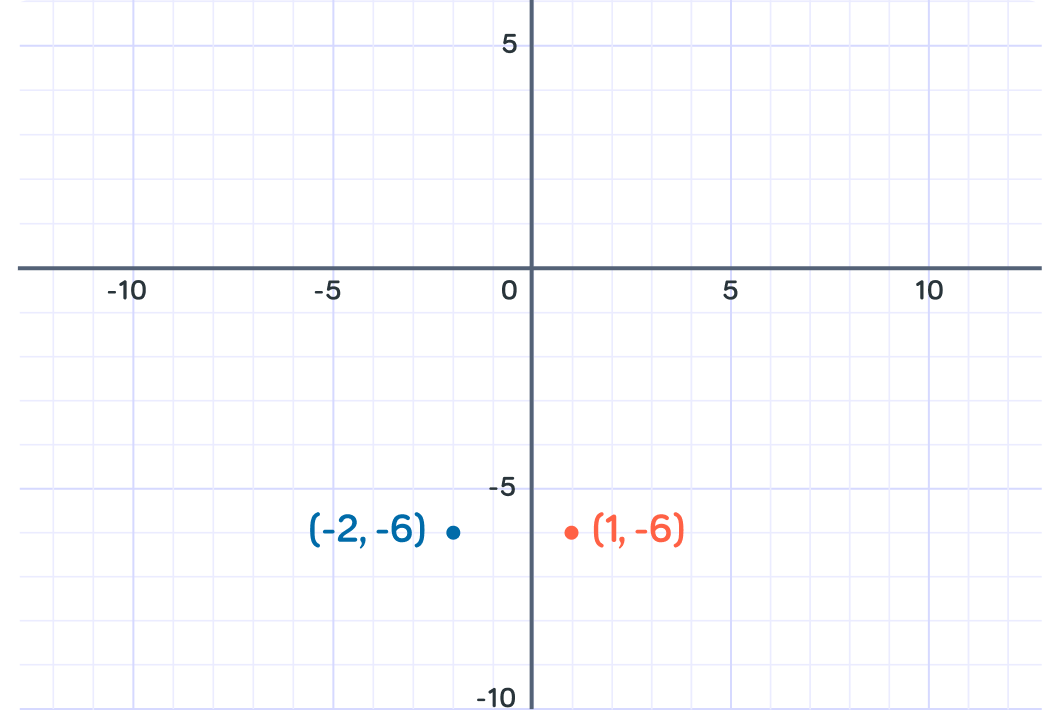
What is $y$ when $x=-2$ ?

When $x=-2$ , $y=-6$

This is because $y=-2^3-2(-2^2)-5(-2)$ . Remember that a negative multiplied by a negative equals a positive. We can plot this point at $(-2,-6)$

What is $y$ when $x=2$ ?

When $x=2$ , $y=-10$ $y=2^3-(2 \times 2^2)-(5 \times 2)=-10$ .

We can plot this point at $(2,-10)$ . Let's try filling out a few more values in a table.

The graph of $y = x^3 -2x^2 -5x$

We can use a table of values to help find points which will allow us to draw a cubic graph.

In this table we can see the points we have already calculated for when $x= -2, 1, 2$ .

Let's fill this table out so we have more points to help us find the curve. What is the y-coordinate for when $x=-1$ ?

What is the y-coordinate for the point when $x=3$ ?

What will be the point when $x=4$ ? Give your answer in the form $(x, y)$ .

Nice!

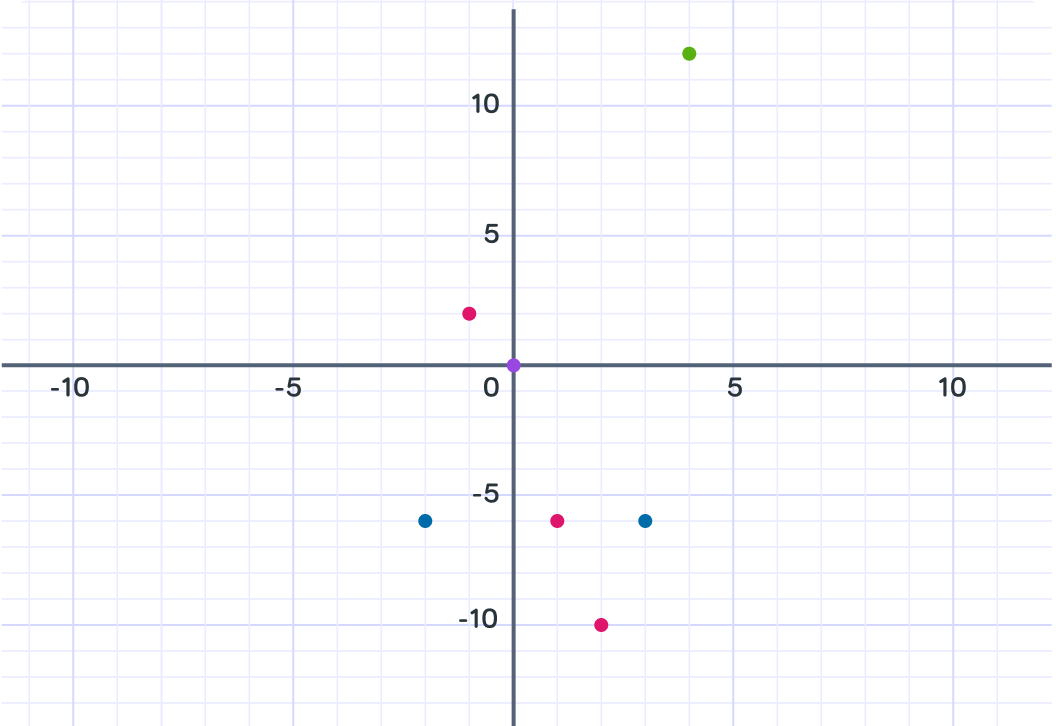
Now we have enough points to draw a line.

the graph of $y = x^3 -2x^2 -5x$

Here we can see all the points we calculated plotted on the graph.

Now all we need to do is join these points up with a smooth curve.

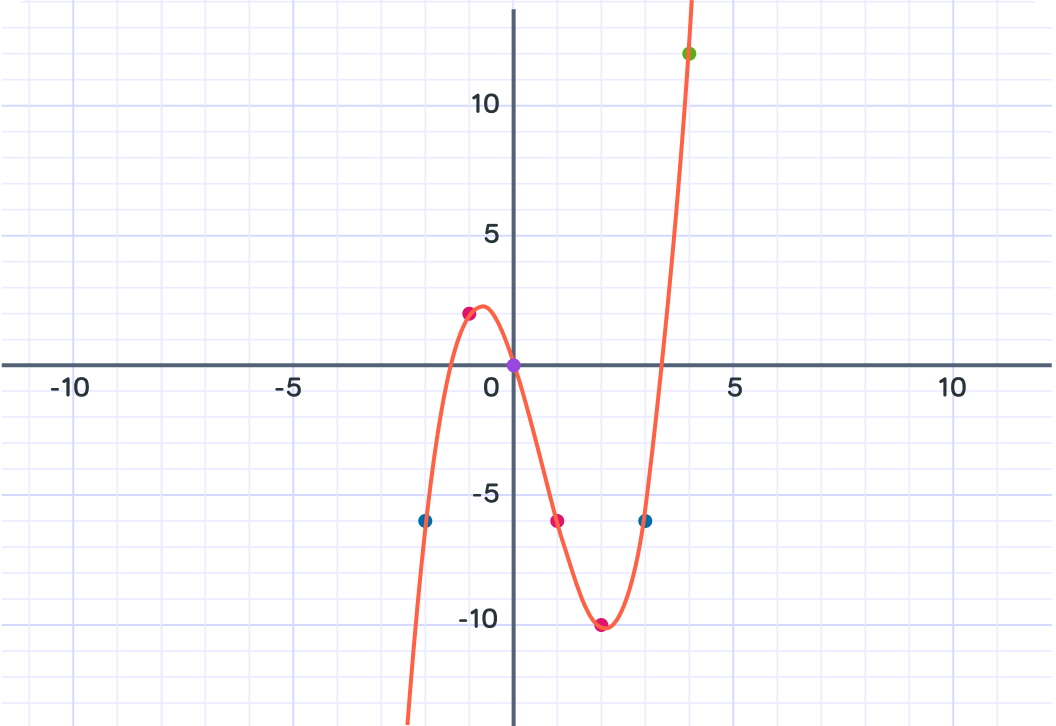
Awesome!

This is the line of $y=x^3-2x^2-5x$ .

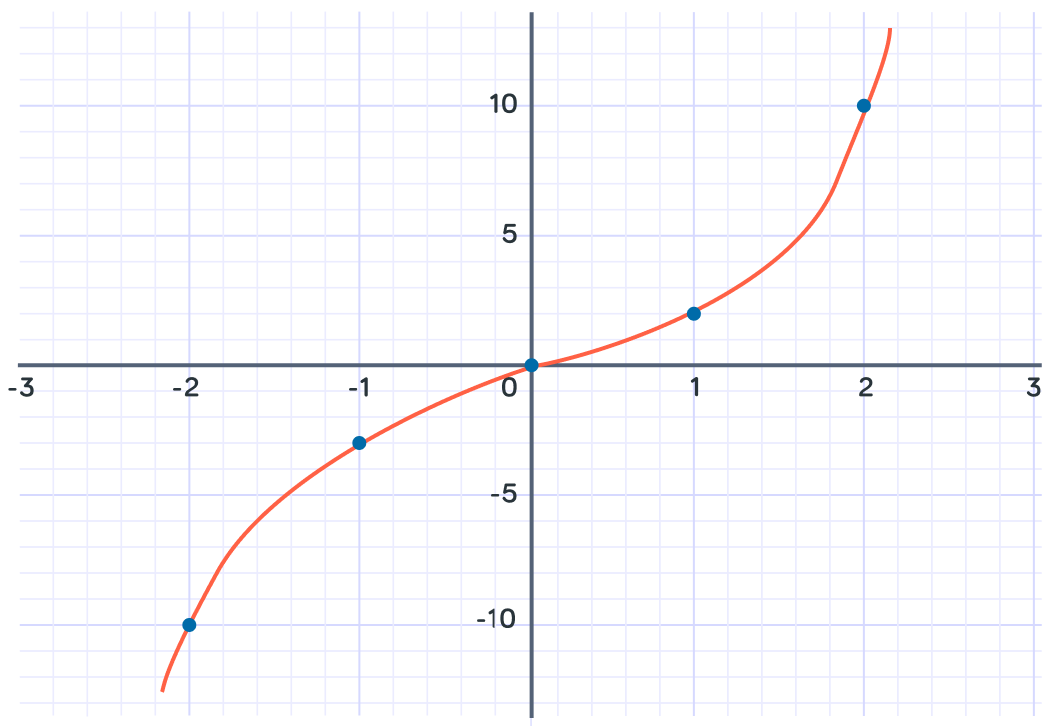
Let's draw the curve of $y = x^3 + x$

Remember, we can find values of $y$ by substituting values of $x$ into the equation.

Let's give it a go

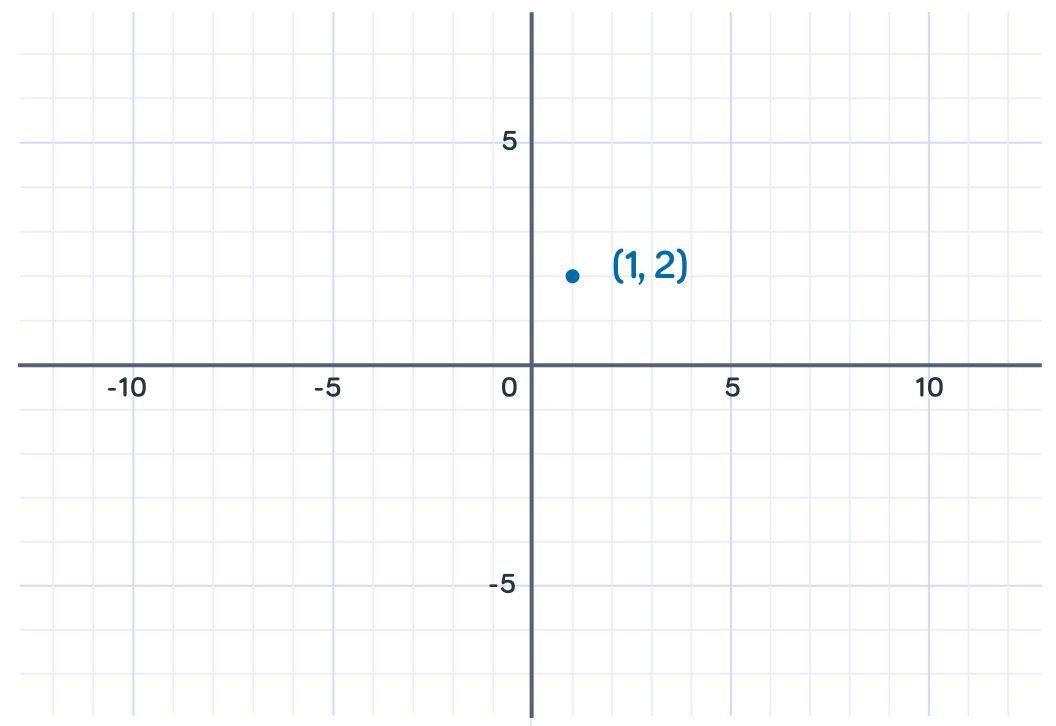
What is $y$ when $x=1$ ?

What is $y$ when $x=-1$ ?

Does the curve pass through the origin, $(0,0)$ ?

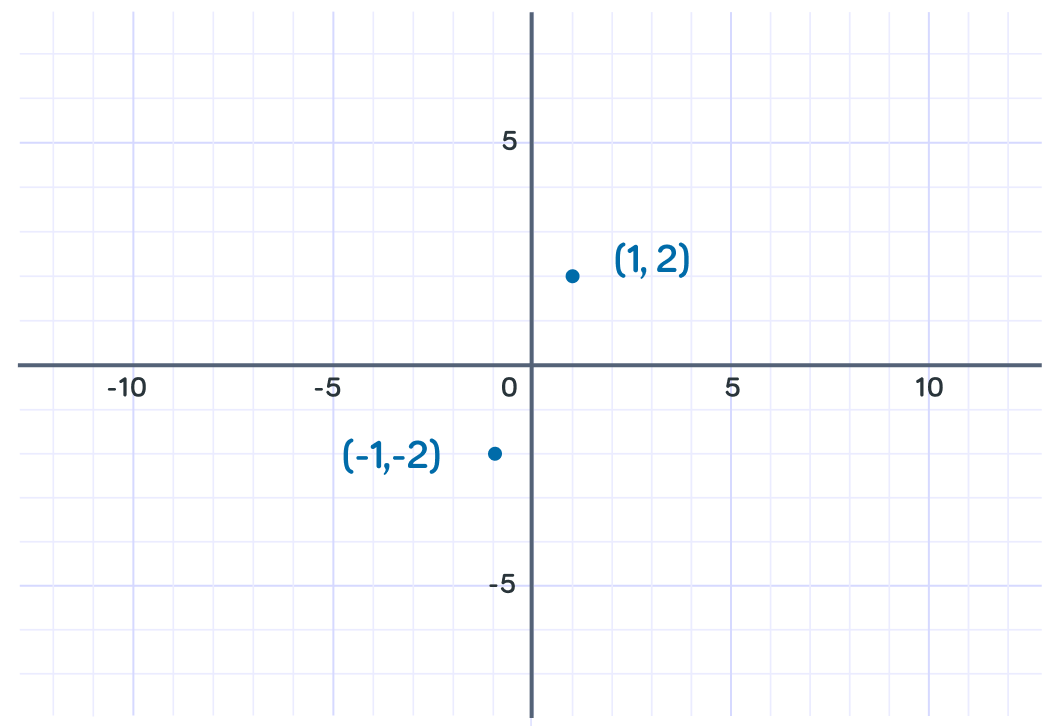
What is $y$ when $x=-2$ ?

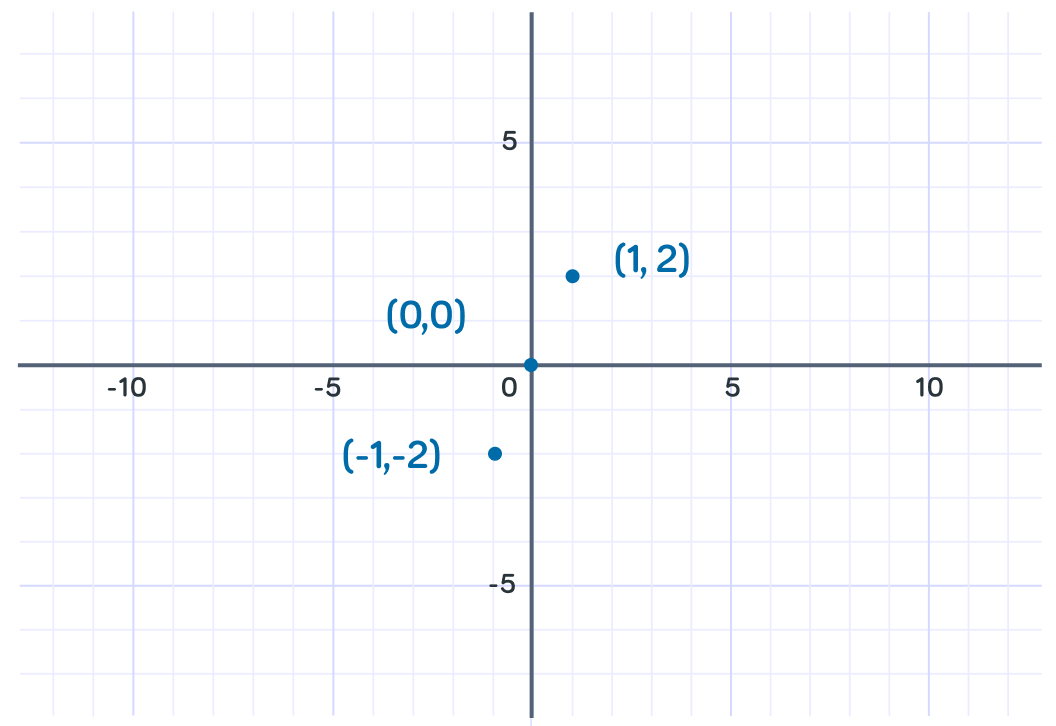
Awesome! We have enough points

Now we can draw a line to smooth join the points together.

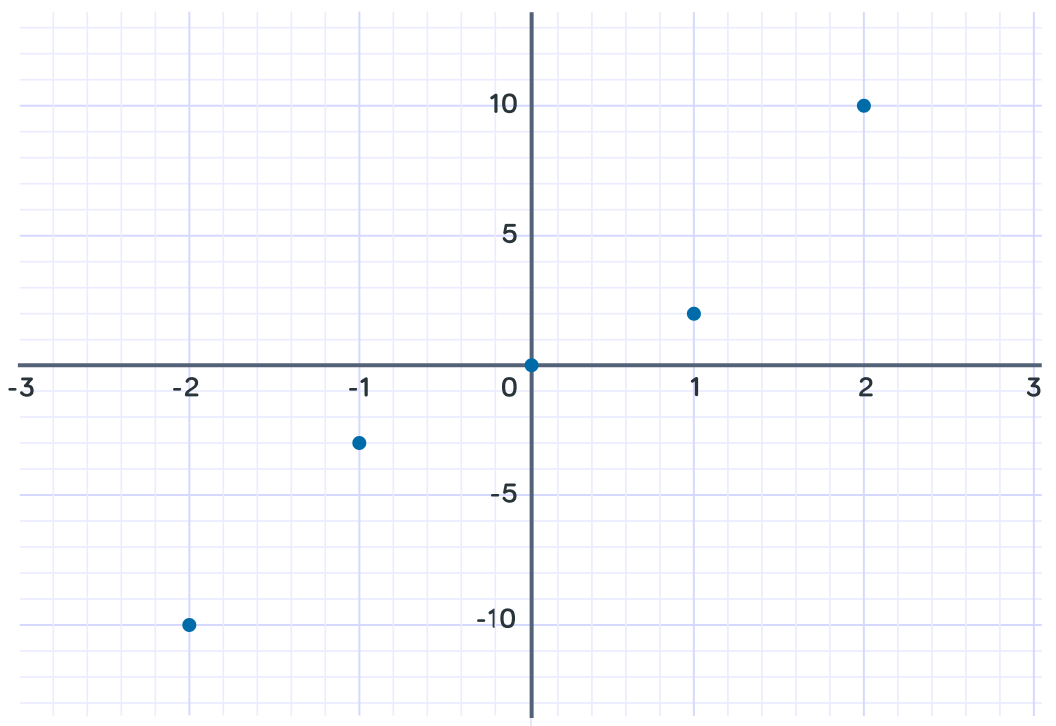
This is the line of $y=x^3+x$

Nice!