Graphs

YOU ARE LEARNING:

Exponential Functions

Exponential Functions

Exponential functions describe situations where the rate of growth is constantly increasing or decreasing. This is a powerful concept that appears in areas like investments and cell growth, as exponential growth and decay.

Sometimes, quantities increase or decrease at a rate which is not constant. For example, you started out as a single cell. The number of cells has grown exponentially over your life to include the trillions of cells that make your body up today!

Algebraically, an exponential function is an equation of the following form, where $a$ can be any number. When $x$ is positive, this is called exponential growth

$y = a^x$

Conversely, when the value of $x$ is negative, the function describes exponential decay. The general equation for exponential decay is:

$y = a^{-x}$

Let's calculate a few more points for $y=2^{-x}$ .

What is $y$ when $x=2$ ?

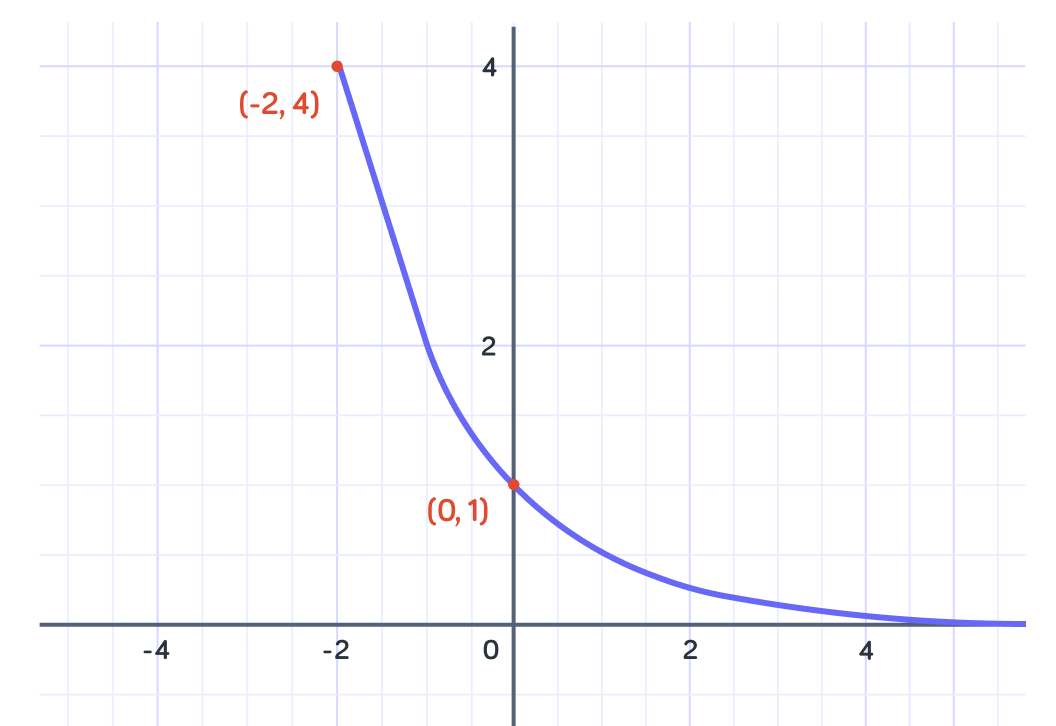
When $x=2$ , $y=\dfrac{1}{4}$

Remember your negative indices! For $x=2$ , $y=2^{-2}=\dfrac{1}{2^2}=\dfrac{1}{4}$ .

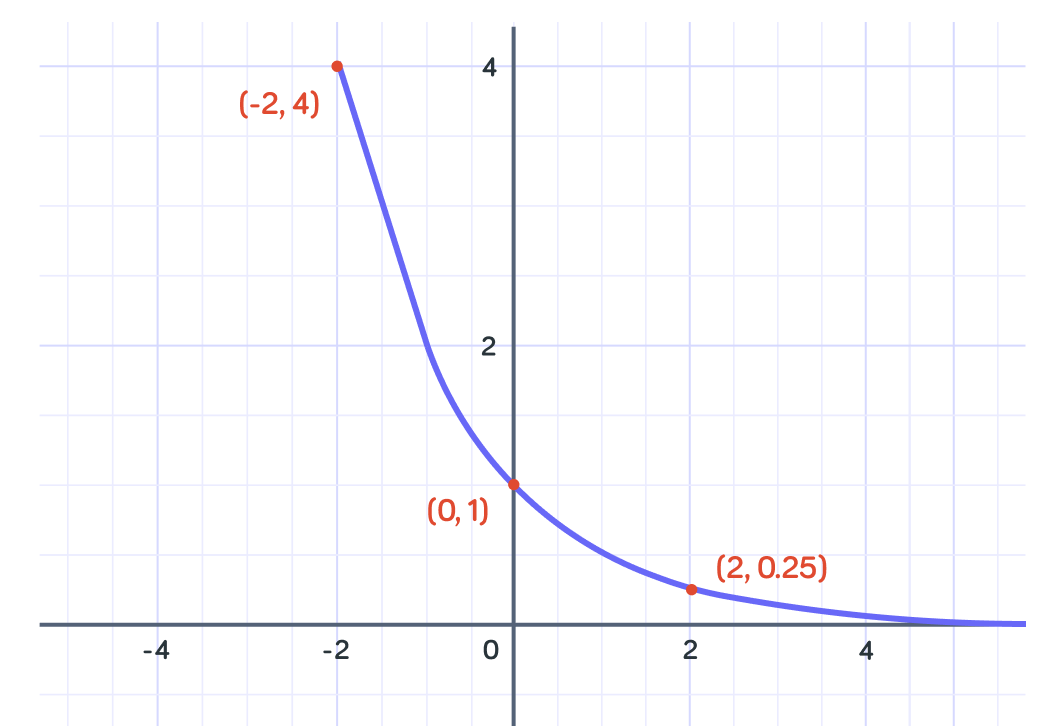
What will $y$ equal to when $x=-1$ ?

And what will the y-coordinate be for when the x-coordinate is $1$ ?

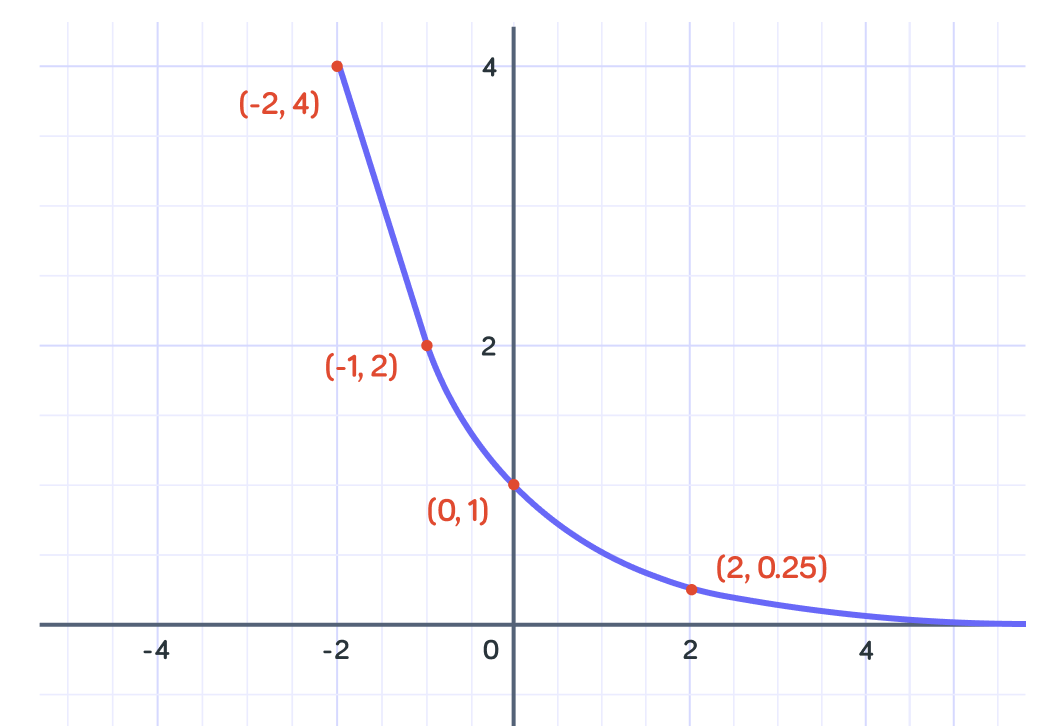
Nice!

We can see these points represented on the graph.

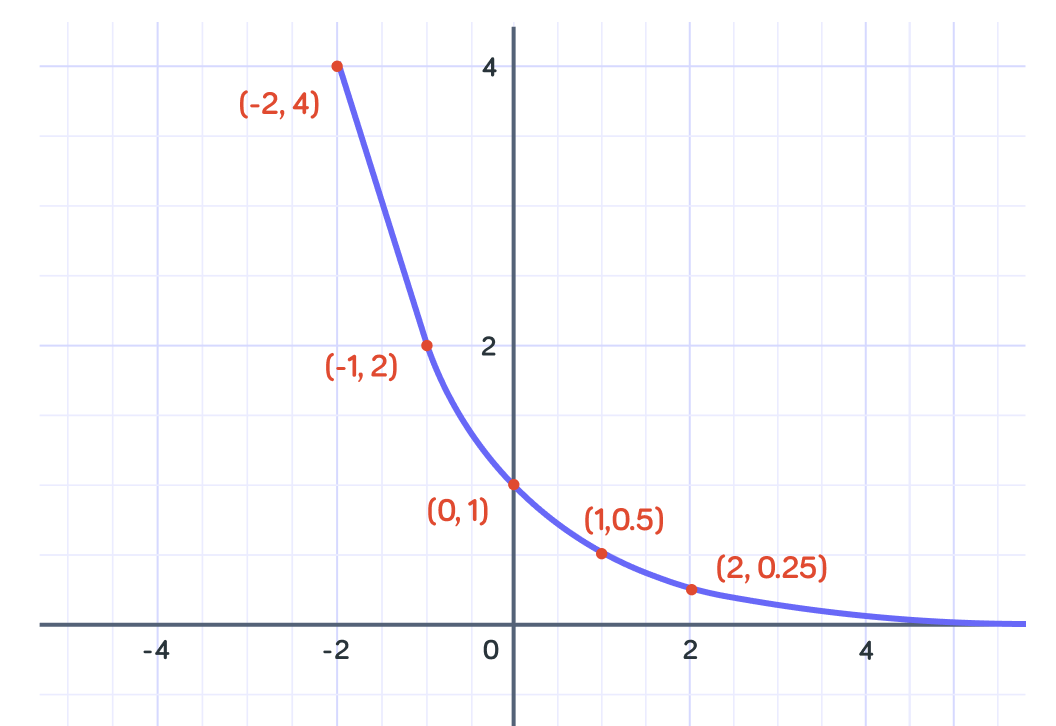
Both exponential growth and decay can be used to model situations in real life.