YOU ARE LEARNING:
Quadratic Graphs

Quadratic Graphs
Quadratic graphs are curved graphs where the highest power of x is 2. We use a table of values to figure out each point on the graph.
Quadratics are any graph where the highest power of x is x2. They have a distinctive U-shaped curve, which is symmetrical.
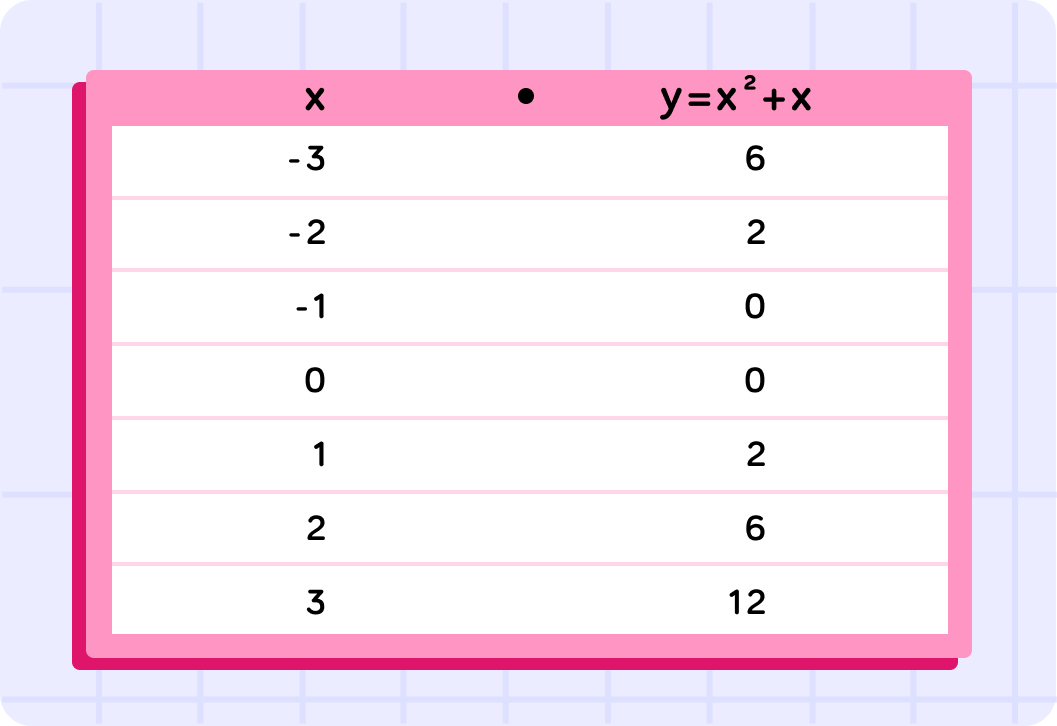
Let's try the equationy=x2+x
This means that for every x value....
... y is the square of x plus x
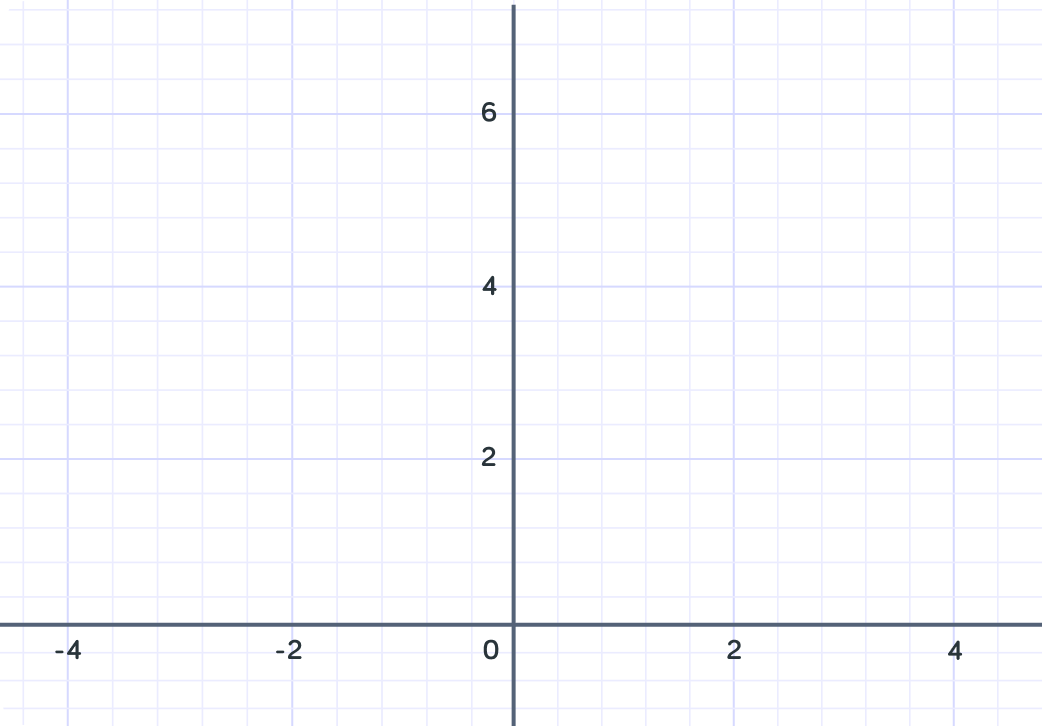
What is y equal to when x=0 ?


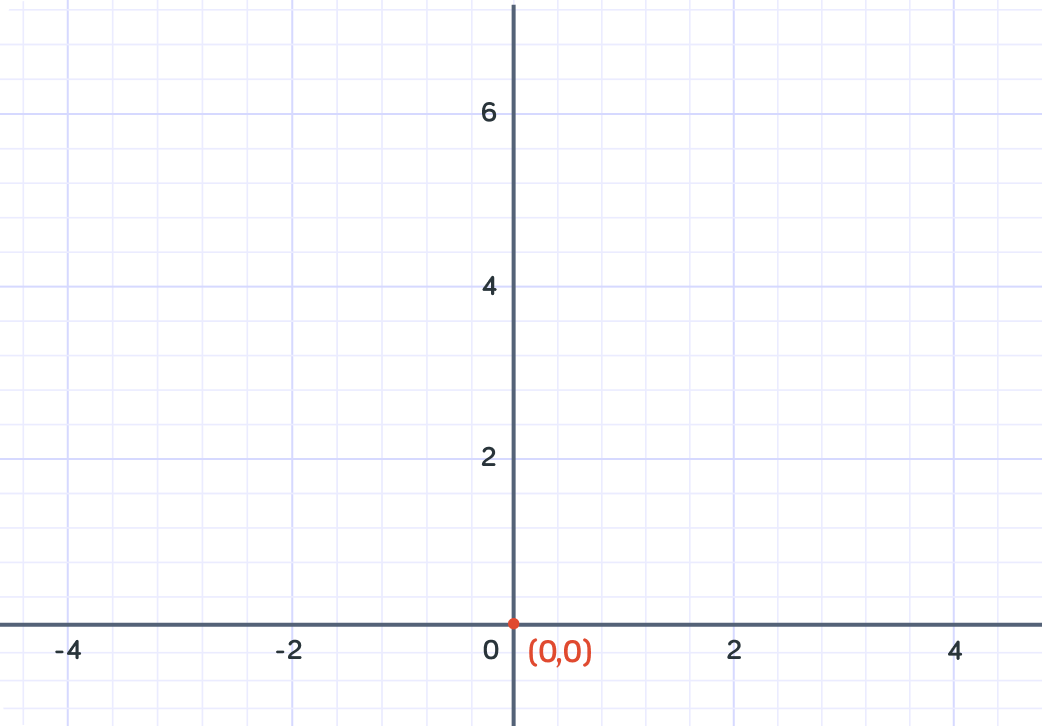
So when x=0 , y=0
We can plot this point on the graph at the coordinates (0,0) .
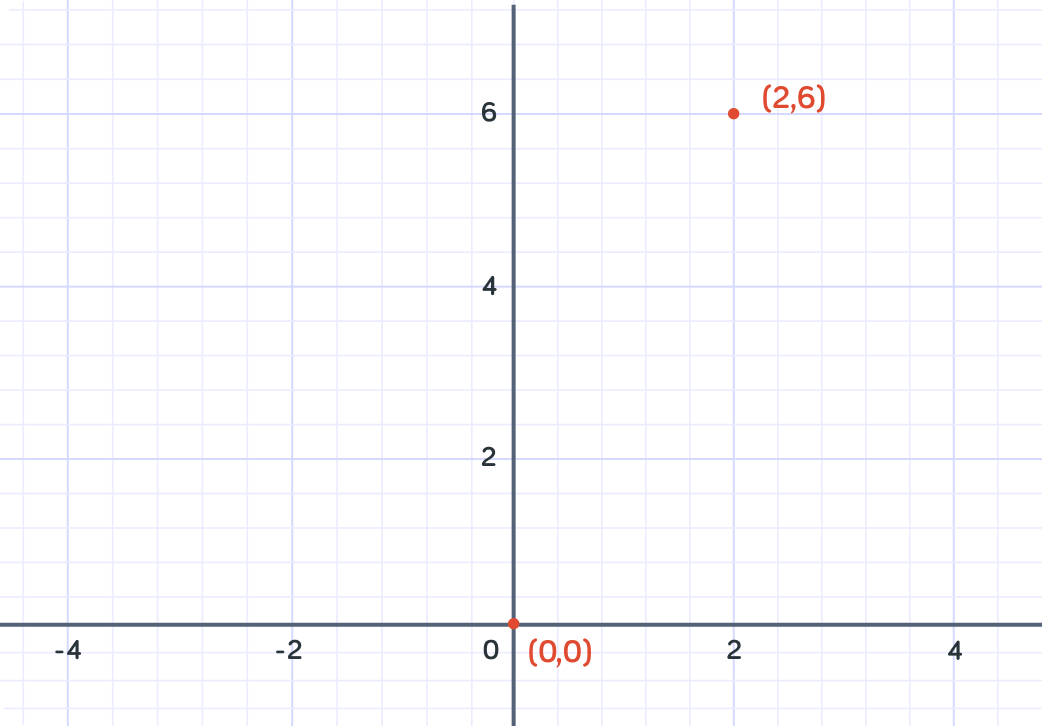
What isy when x=2 ?


So when x=2 , y=6
We can plot this point on the graph at the coordinates (2,6)
What is y when x=−1 ?


So when x=−1 , y=0
We can plot this point on the graph at the coordinates (−1,0) . Notice that the line crosses the x-axis twice!
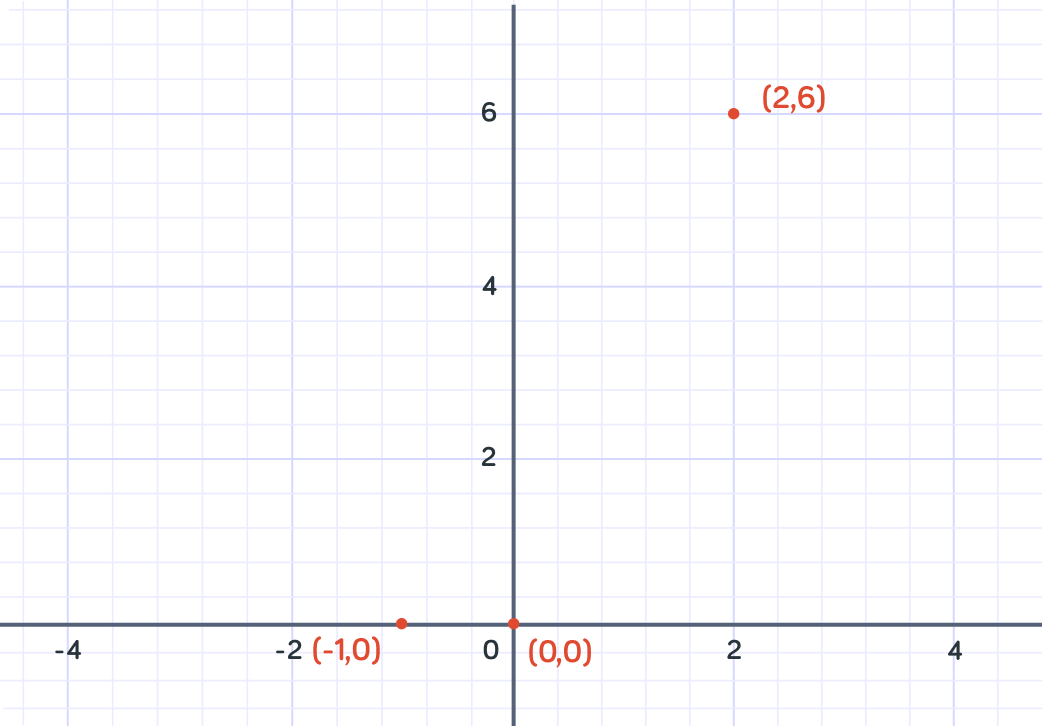
Let's calculate one more point. What is y when x=−3 ?


Nice!
Now we have enough points to join up to find the line y=x2+x
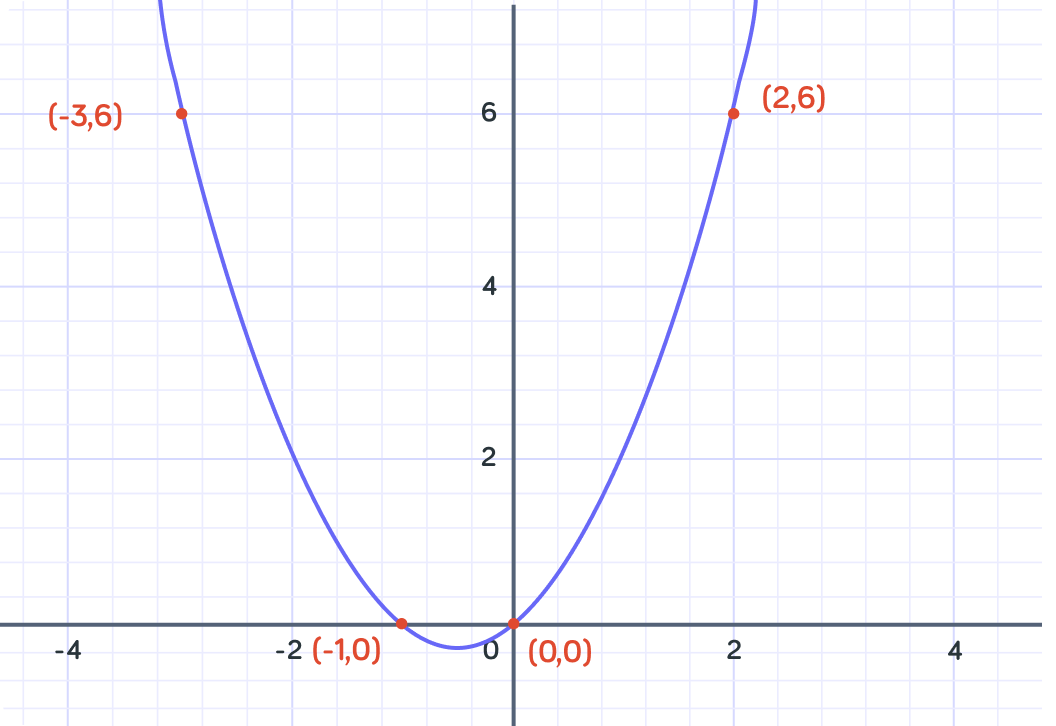
The easiest way to draw a quadratic is by first completing a table of values, then plotting the points and joining them up with a smooth curve.
In the table above we can see the values for y=x2+x that we have already calculated.
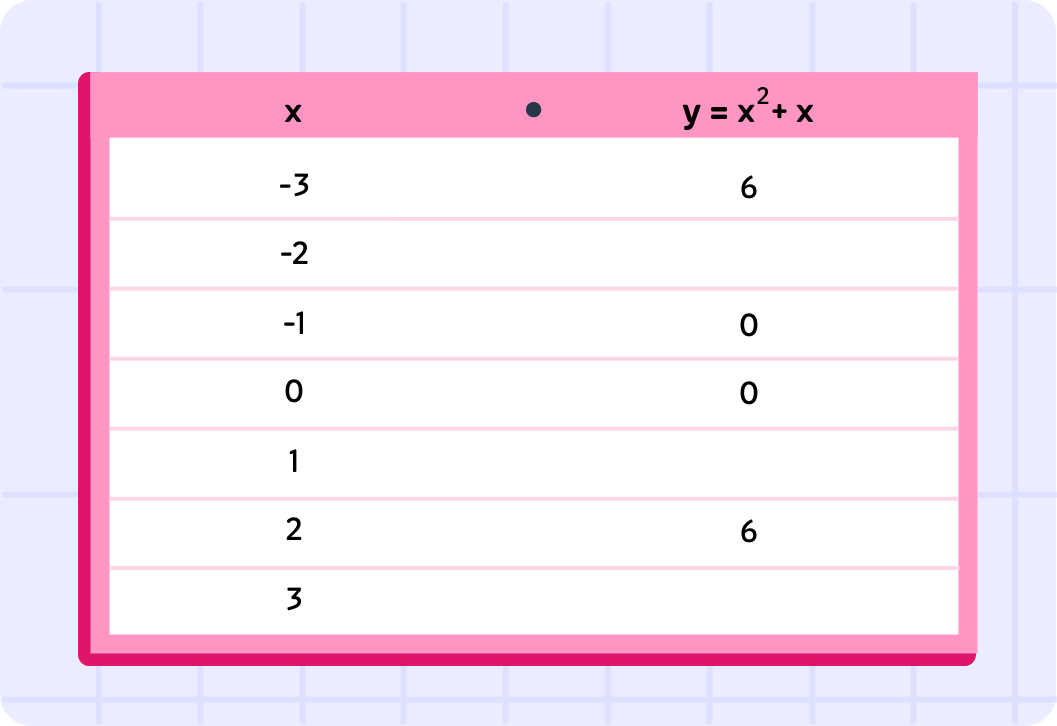
Some values of y are missing. What is y when x=−2 ?


What will the y-coordinate be for when the x-coordinate is 1?

Finally, what will the point be along the curve at x=3 ? Give your answer in the form (x,y).

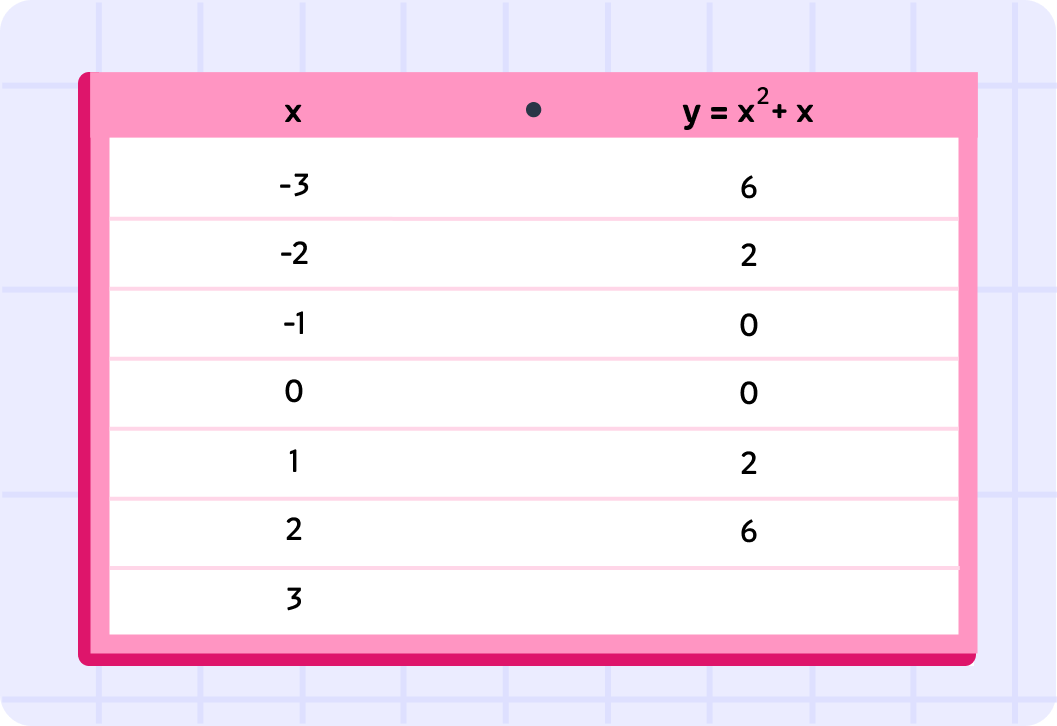
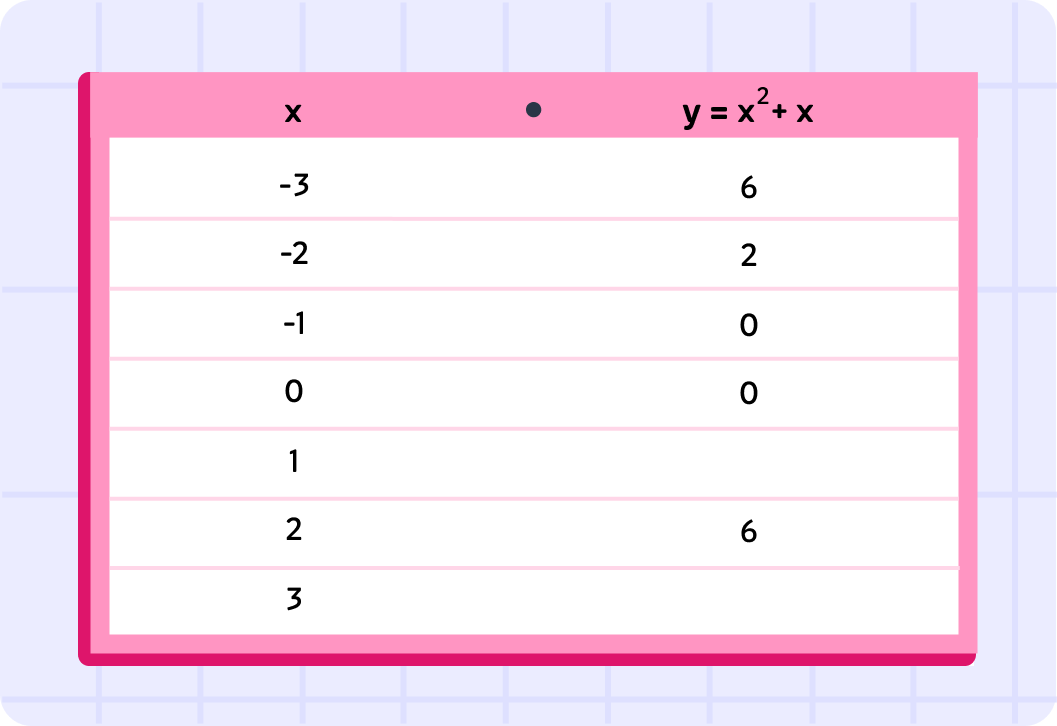
So here is the completed table of values for y=x2+x.
You might notice that the values are symmetrical around x=−1,0. This is because the line is a symmetrical curve!