Graphs

YOU ARE LEARNING:

Reciprocal Graphs

Reciprocal Graphs

Reciprocal graphs contain x as the denominator of a fraction, and have a very distinct symmetrical shape.

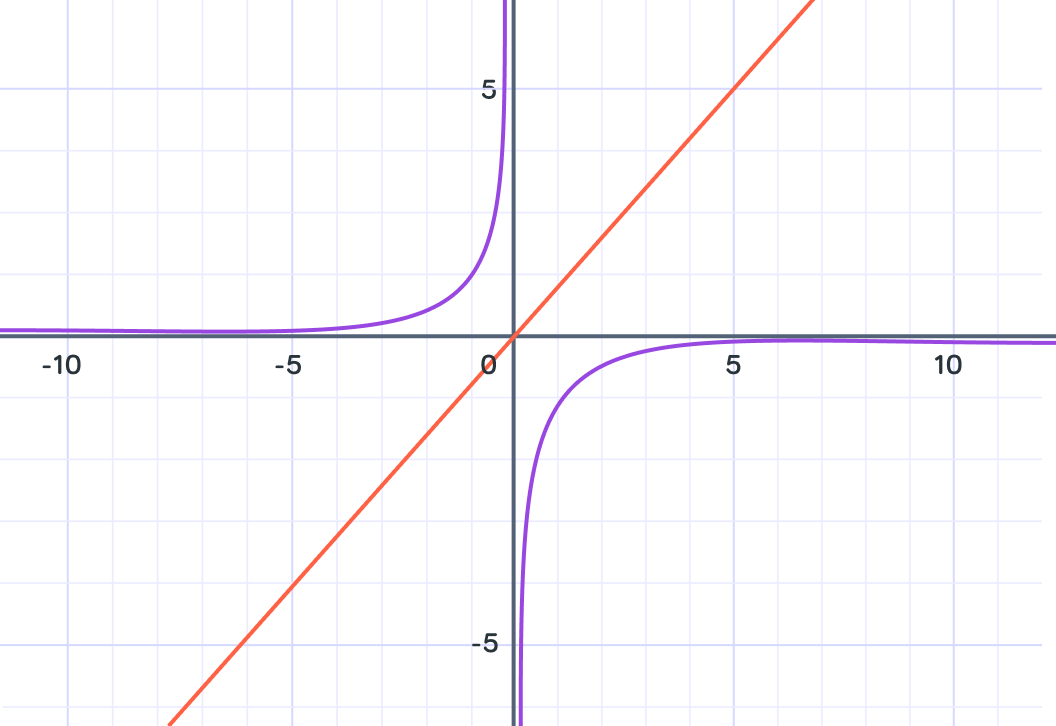
Reciprocal graphs describe functions which contain $x$ in the denominator. They have a distinctive shape with two separate lines which are symmetrical to each other.

It is symmetrical about the line $y=x$

Look at the graph above to see this illustrated.

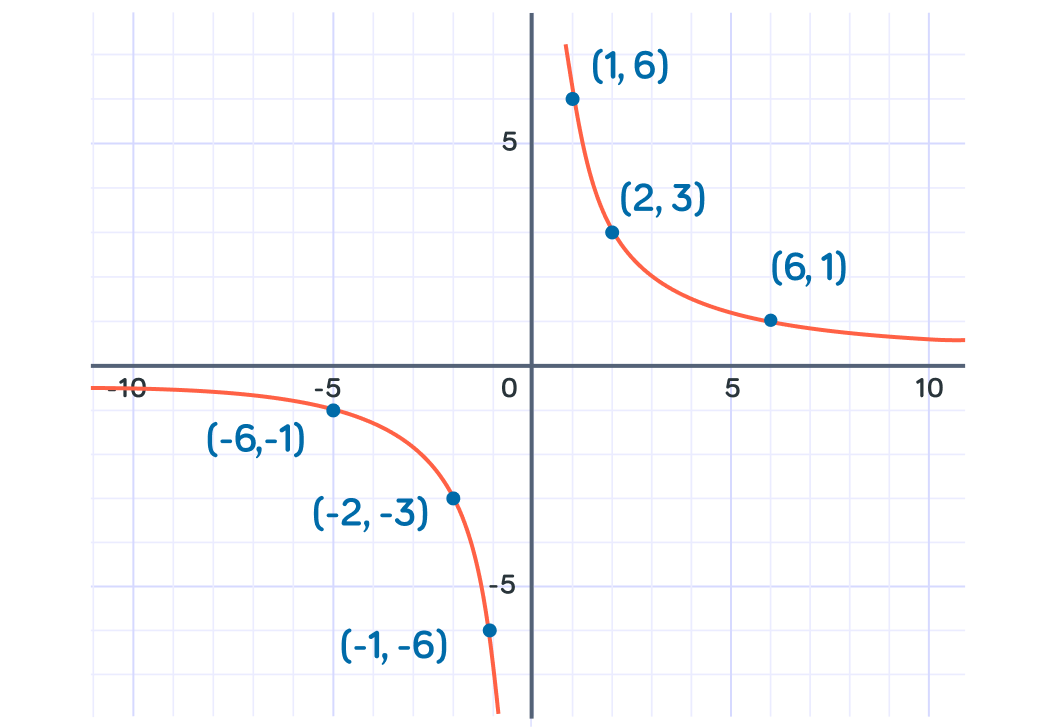
Let's now find some points for the curve $y=\frac{6}{x}$

To do this, we substitute into the equation values for $x$

and then calculate the corresponding value of $y$ .

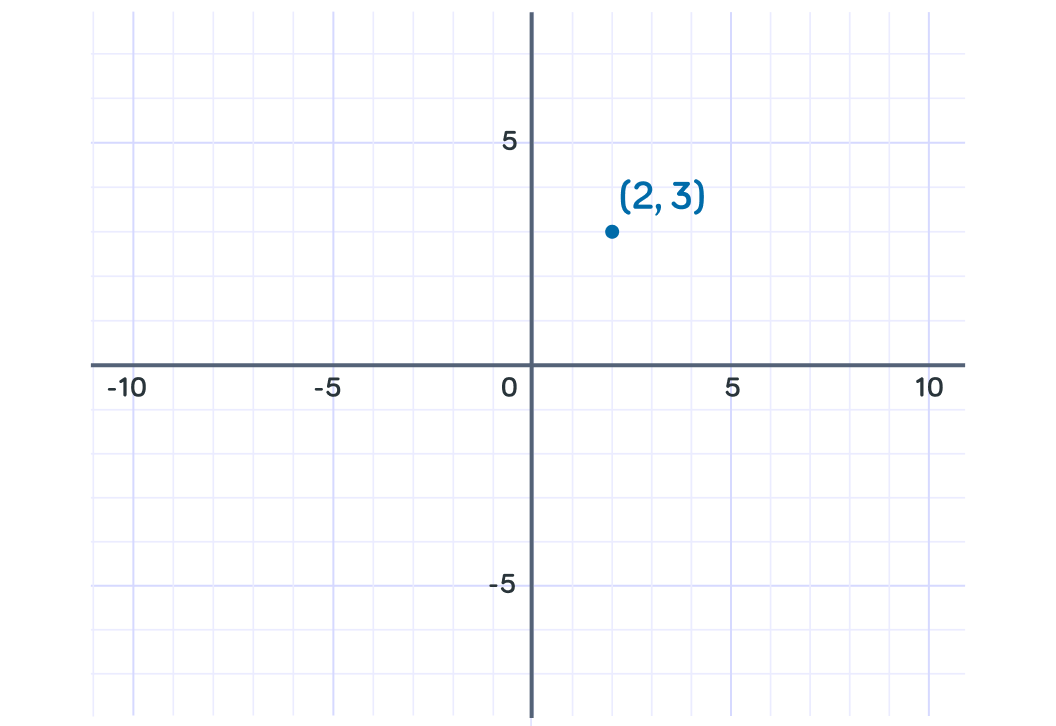
What will $y$ equal to when $x=2$ ?

So when $x=2$ , $y=3$

We can now plot this point $(2, 3)$ on the graph.

What is $y=\frac{6}{x}$ when $x=1$ ?

So when $x=1$ , $y=6$

We can now plot this point $(1,6)$ on the graph.

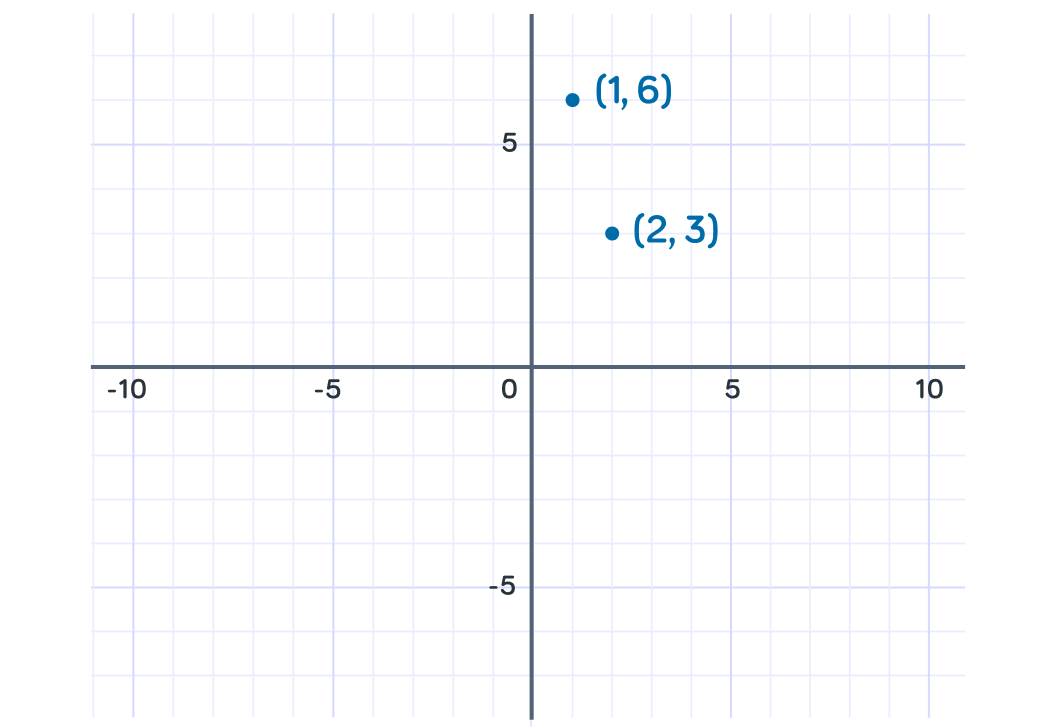
What will $y$ be equal to when $x=6$ ?

Will the curve $y=\frac{6}{x}$ pass through the origin, $(0,0)$ ?

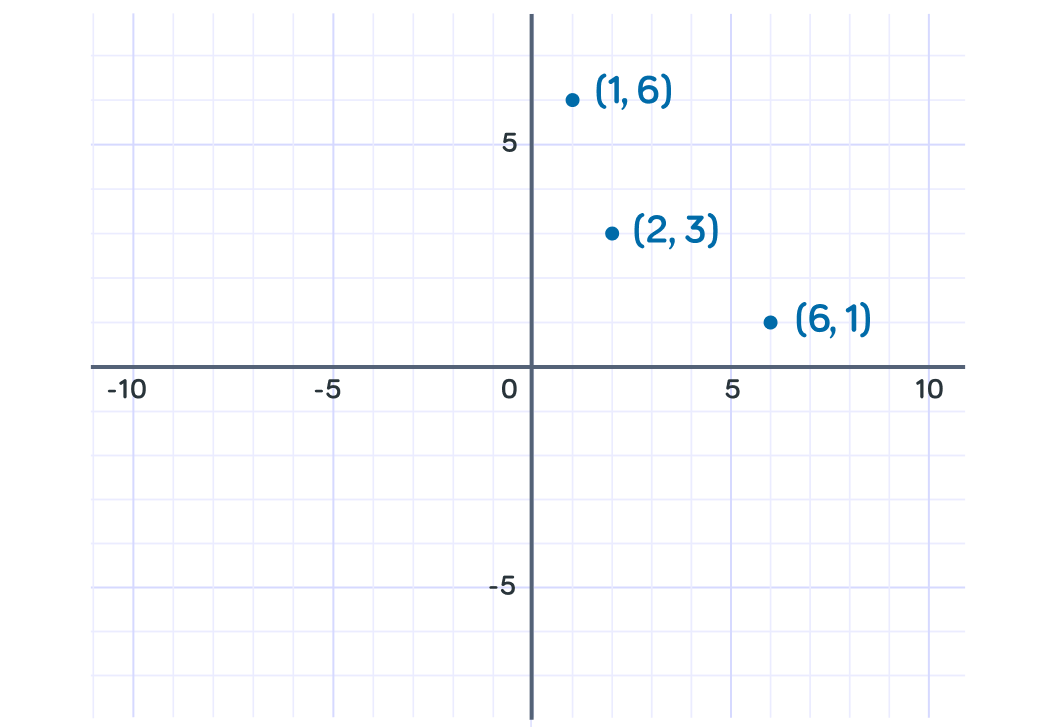
We know that the curve will not touch either of the axes so we can join these points up, and continue the line so that it runs along the axes with touching them.

This gives us half of the graph. There is also another curve in the opposite quadrant to be drawn.

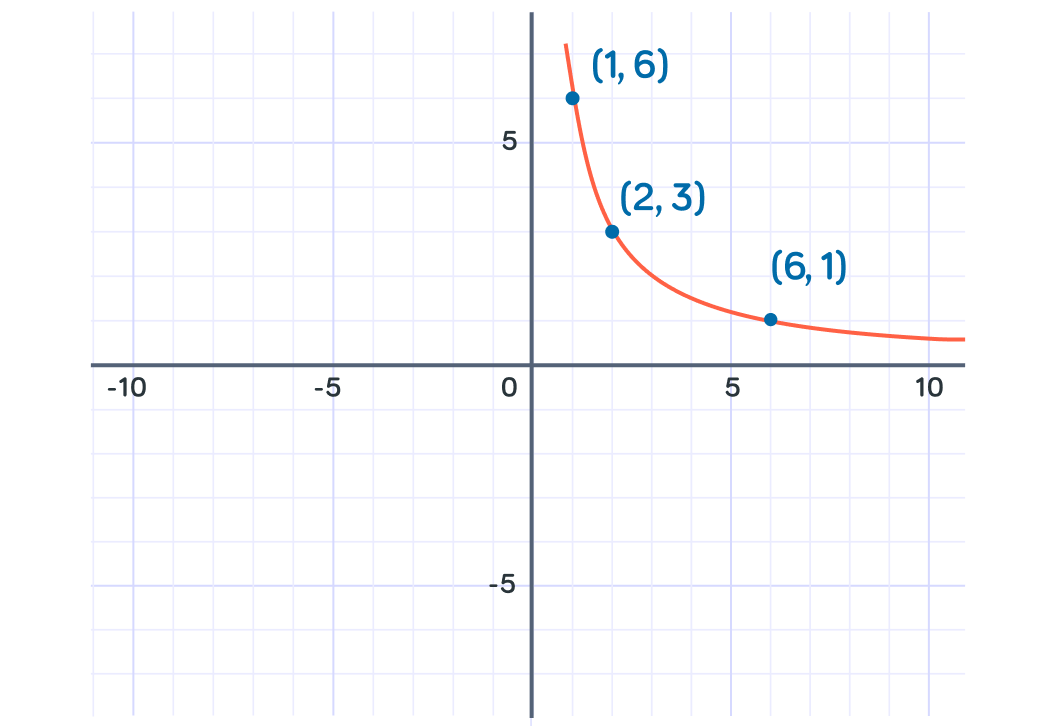
To find the other half, we can simply mirror the points along the line y=-x.

This is the same as making all of the points negative.