Number

YOU ARE LEARNING:

Highest Common Factors

The highest common factor is the highest number which is a factor of two other numbers. We can use prime factorisation to find it.

What is a factor of a number?

Which of these are factors of $36$ ? Select all that apply.

You can select multiple answers

A common factor of two numbers is a factor that divides into both numbers without leaving a remainder. Which of these is a common factor of $36$ and $51$ ?

Finding the highest common factor, or HCF, of two numbers can help when working with fractions.

We find the HCF using prime factorisation.

Let's try an example.

What is the HCF of $30$ and $75$ ?

First we find the prime factorisation of each number.

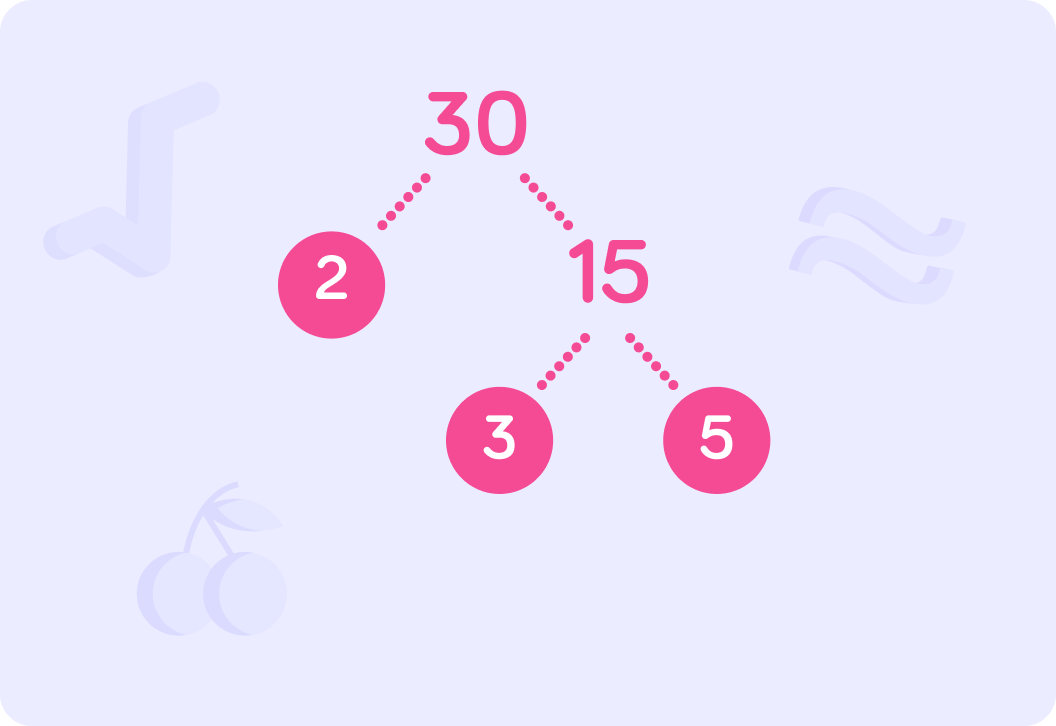
This is the prime factorisation tree for $30$ .

Using a prime factorisation tree, find the prime factors of $75$ .

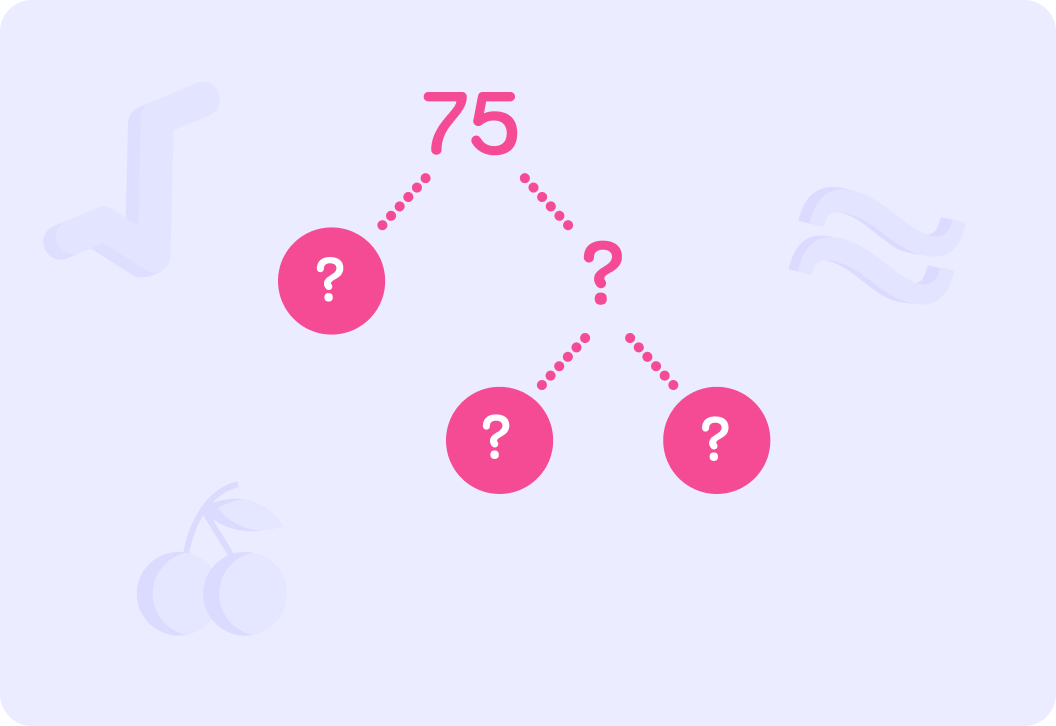
We now have the prime factorisations of both $30$ and $75$ . One common factor is $3$ , what is the other?

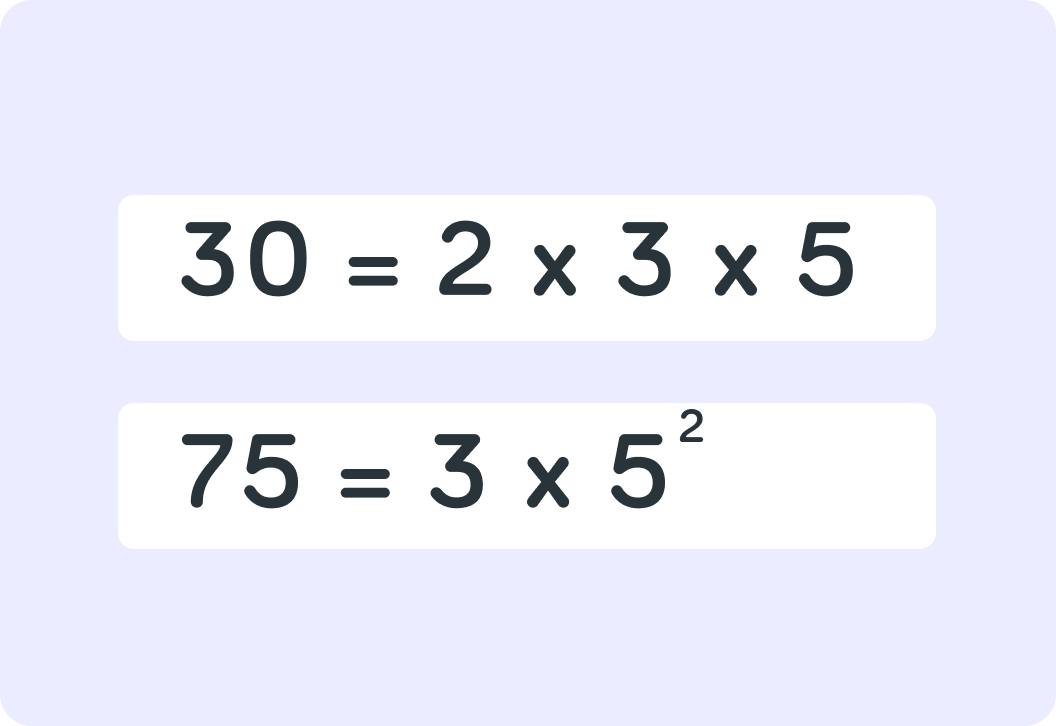
We have identified that $3$ and $5$ are common prime factors of $30$ and $75$ . How can we find the highest common factor?

The common prime factors are highlighted, what is the highest common factor of $30$ and $75$ ?

Well done! You have found the answer!

The HCF of $30$ and $75$ is $15$ .

When the numbers are smaller, we can list the factors to find the highest common factor.

Let's find the highest common factor of $27$ and $39$ .

We can list the factors of $39$ , they are $1$ , $3$ , $13$ and $39$ . What are the factors of $27$ ? List them in order and separate your answers with a comma.

Now we have all the factors of the two numbers, what is the HCF of $27$ and $39$ ?

The HCF of $27$ and $39$ is $3$ .

With this method, when listing the factors we just find the highest one, there is no multiplying needed!

Quick recap - which option describes the HCF?

How can you find the HCF by listing the factors of each number?

What is the highest common factor of $15$ and $35$ ?

Fred says that $8$ is the HCF of $24$ and $48$ . Is he correct? If not, what is the HCF of $24$ and $48$ ?

We've seen that the HCF of $24$ and $48$ is $24$ .

This shows that sometimes the HCF of two numbers is the smaller of the two numbers.

What is the HCF of $36$ and $180$ ?

You may need some time to work this out

Let's try a harder example: finding the HCF of three numbers.

Let's find the HCF of $200$ , $60$ and $40$ .

The prime factorisation of $200$ is $2^3\times 5^2$ . What is the prime factorisation of $60$ ?

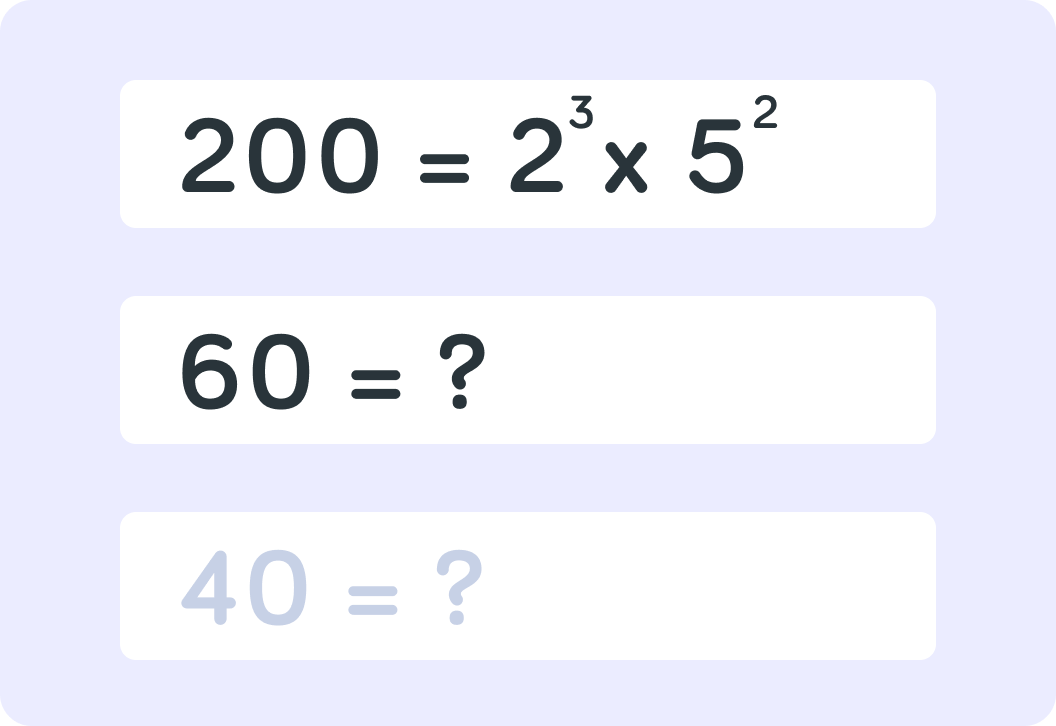
We need to find our final prime factorisation of $40$ , what is this one?

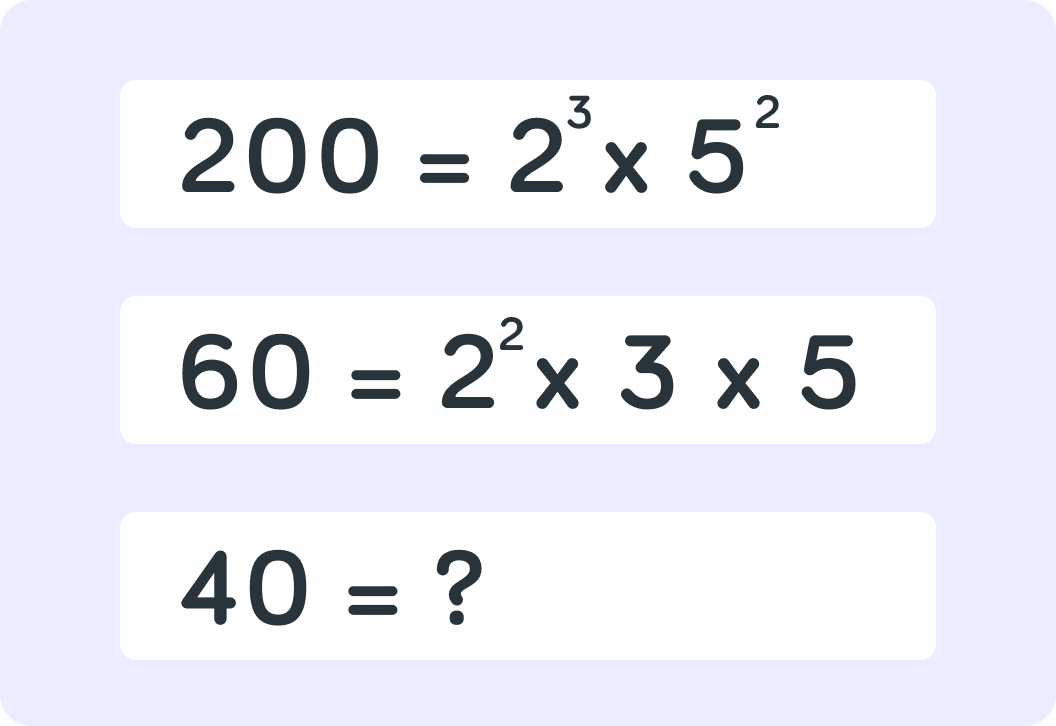
We now have the prime factorisations for all three numbers.

We need to compare them and find which are common to all three numbers.

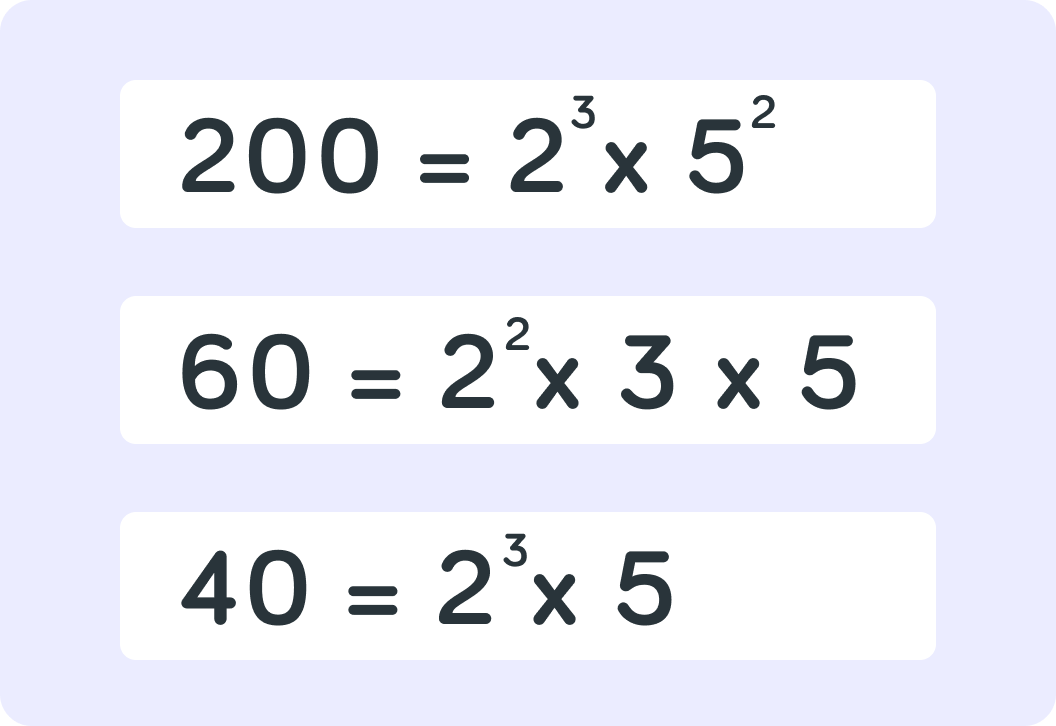
Which two prime numbers appear in all three? Separate your answers with a comma.

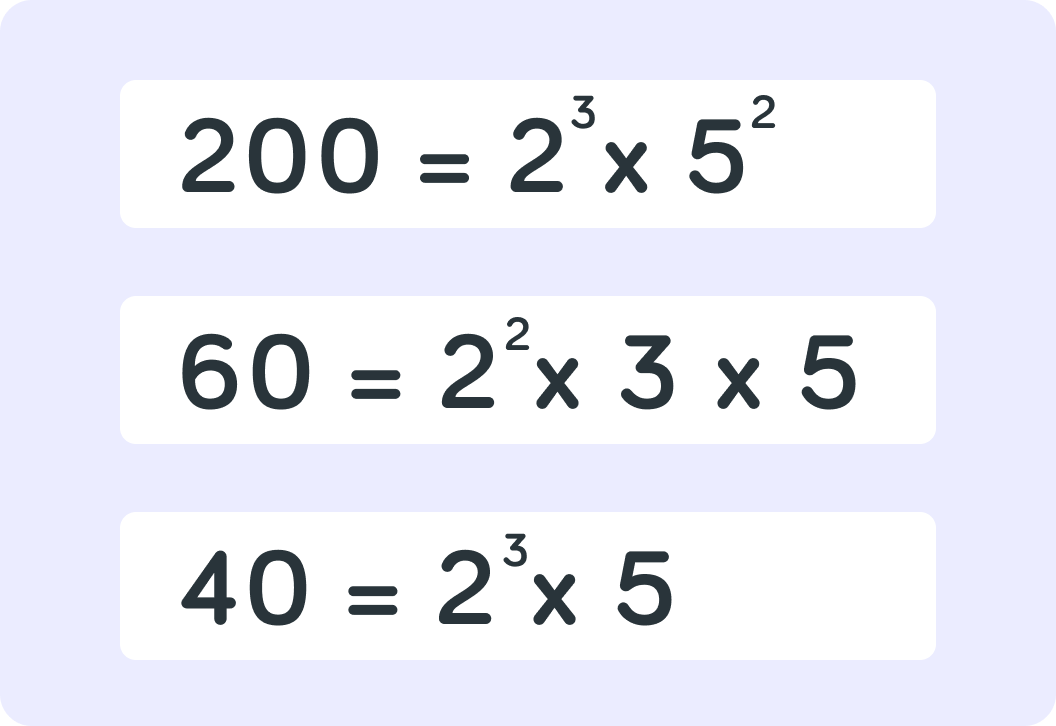
Be careful with this one! We identified that the common prime factors are $2$ and $5$ , but look more closely at the $2$ . What is the actual common factor here?

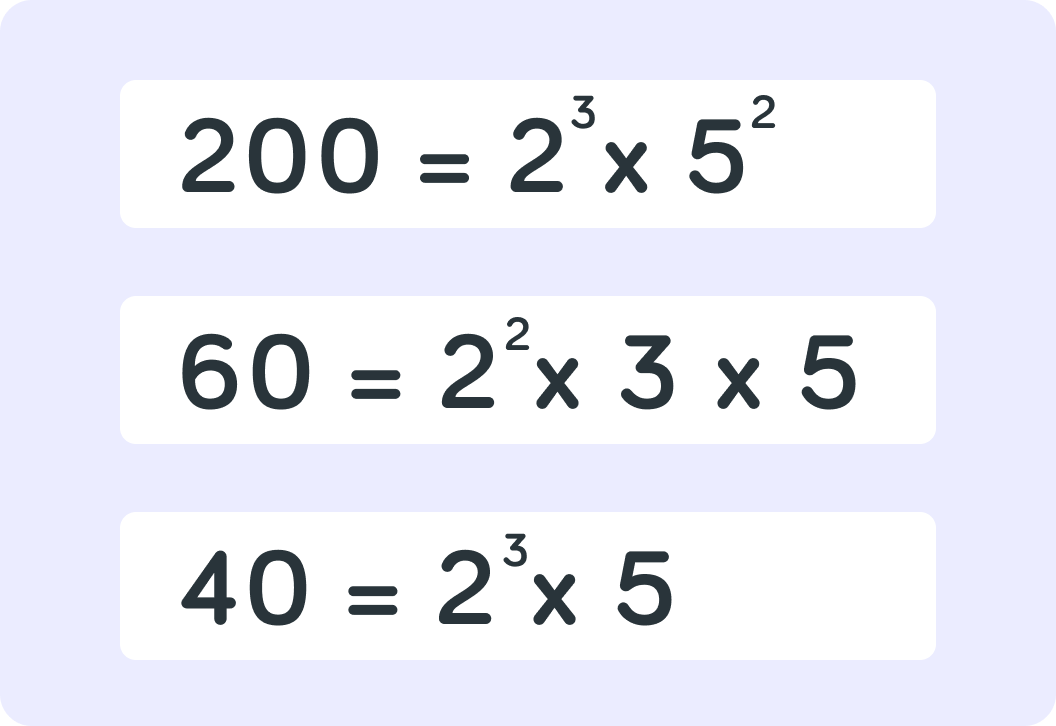
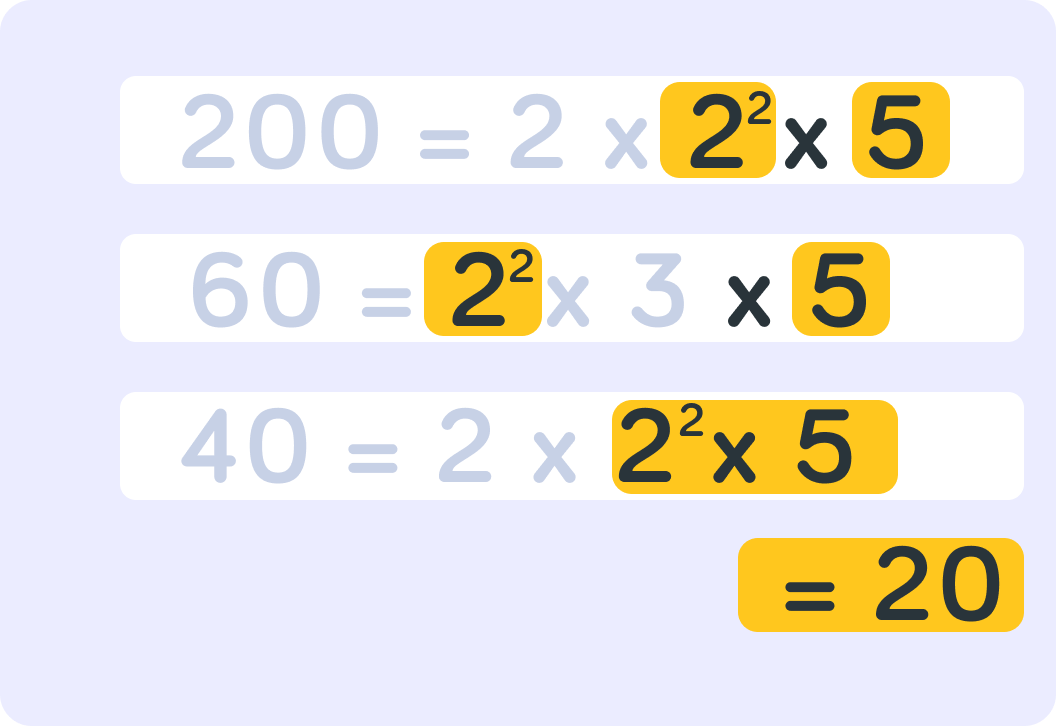
Now let's find out HCF of $200$ , $60$ and $40$ . The common factors are $2^2$ and $5$ , what is the HCF?

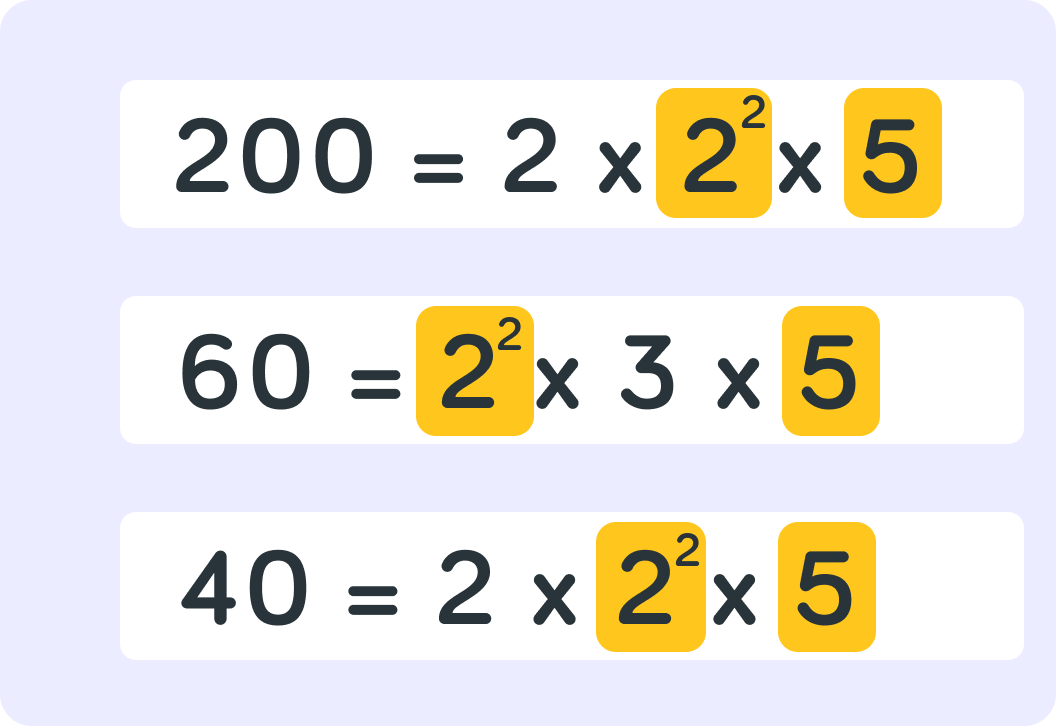
Well done! The HCF of $200$ , $60$ and $40$ is $20$ .

Where a common prime factor has a power, we choose the lowest power to find the HCF.

Summary!

A factor is a number which divides into another number exactly, leaving no remainder, decimal or fraction.

$5$ is a factor of $20$ because $20\div 5=4$

$8$ is not a factor of $20$ because $20\div 8=2.5$

A common factor of two numbers is the same factor that divides exactly into both numbers.

$3$ is a common factor of $75$ and $27$ because $75\div 3=25$ and $27\div 3=9$

Numbers can have more than one common factor.

Finding the highest common factor of two numbers can help when working with fractions.

Use prime factorisation of the numbers to find the highest common factor.

The prime factors in common multiply together to give the HCF.

To find the HCF of $84$ and $132$ , find the prime factorisation of both numbers.

$84=2^2\times 3\times 7$ and $132=2^2\times 3\times 11$ The HCF is the product of the common factors which is $2^2\times 3=12$

Where a common prime factor has a power

choose the lowest power to find the HCF.

For smaller numbers it may be easier simply to list all the factors of both.

The HCF is the highest factor that appears in both lists.

$12$ has factors $1$ , $2$ , $3$ , $4$ , $6$ and $12$

$18$ has factors $1$ , $2$ , $1$ , $1$ , $1$ and $1$

The highest factor in both lists is $6$ so the HCF of $12$ and $18$ is $6$ .