Number

YOU ARE LEARNING:

Prime Factorisation

Prime Factorisation

AKA the Unique Factorisation Theorem, we can split any number down into a product of prime numbers, where each number has one unique combination!

A factor is a number that divides into another number exactly. Which of these numbers is a factor of $28$ ?

Because $28\div 7=4$ we know that $7$ is a factor of $28$ .

It also shows that $4$ is a factor of $28$ because $28\div 4=7$ .

We have seen that $4$ and $7$ are factors of $28$ . A prime factor, is a factor that is a prime number. Which one of these is a prime factor of $28$ ?

We have found two factors of $28$ and found that $7$ is a prime factor. What other factors are there are of $28$ ? Select all that apply.

You can select multiple answers

We now have all the factors of $28$ .

They are $1$ , $2$ , $4$ , $7$ , $14$ and $28$ .

Finding all the factors of a number can be quite tedious.

We can use a process called prime factorisation to help.

We have seen that all the factors of $28$ are $1$ , $2$ , $4$ , $7$ , $14$ and $28$ . Which of these are prime? Select two and separate your answer with a comma.

We have now found the prime factors of $28$ , they are $2$ and $7$ . Which calculation uses those factors to make $28$ ?

We have found the prime factorisation of $28$ which is $2\times 2\times 7$ .

Note that sometimes a prime factor is repeated.

Prime number factorisation helps us in other areas of maths.

If can help us to find common multiples and factors which in turn help working with fractions.

Let's use a prime factor tree to find the prime factors of a number.

We will identify the prime numbers as they appear.

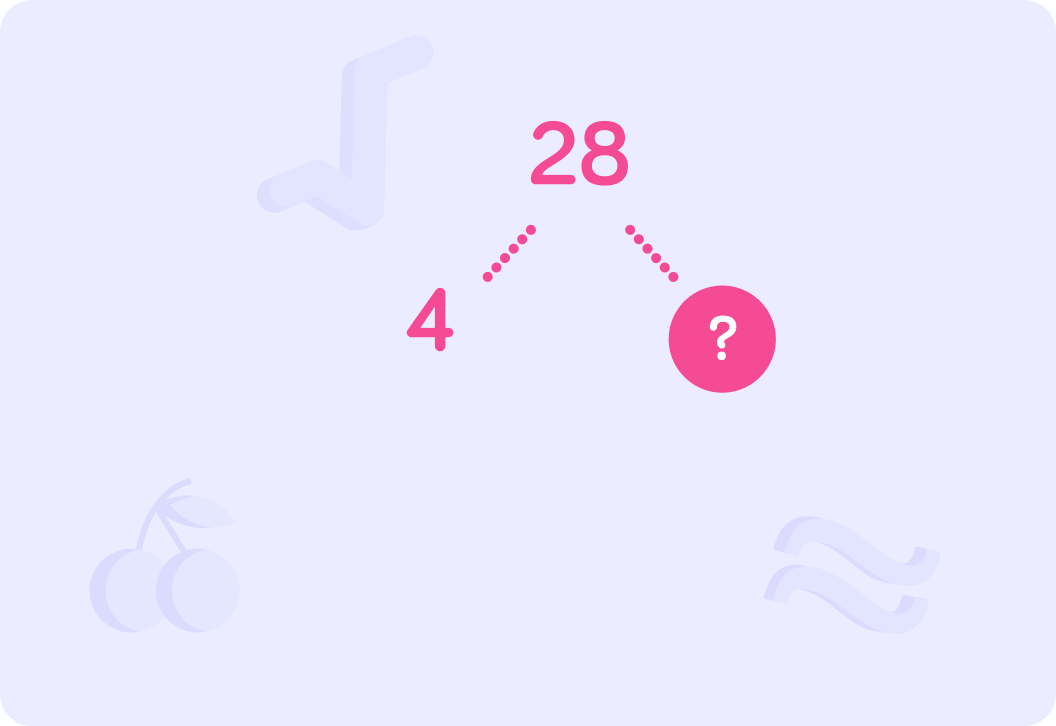
Starting with $28$ , we find a factor. We start with $4$ and put that in the next tier. What number will replace the $?$ ?

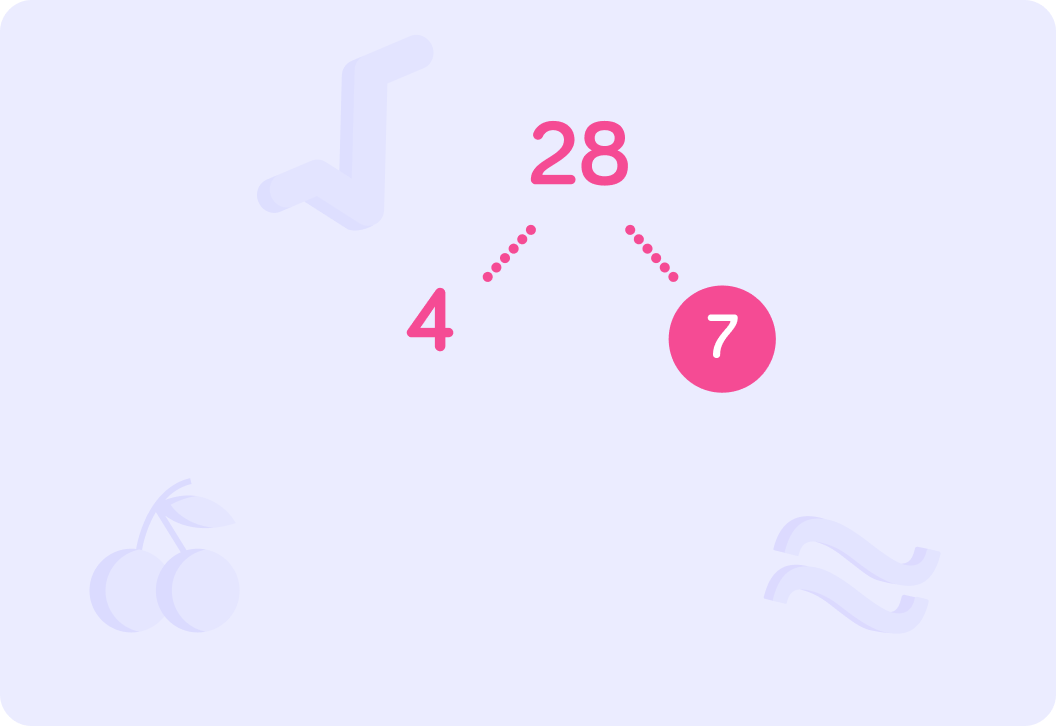
We now look at our factors and determine if either of them is prime.

We know that $7$ is prime, so we circle it to show it is the end of that branch.

We now focus on the number $4$ . What number is a factor of $4$ that can replace both the question marks?

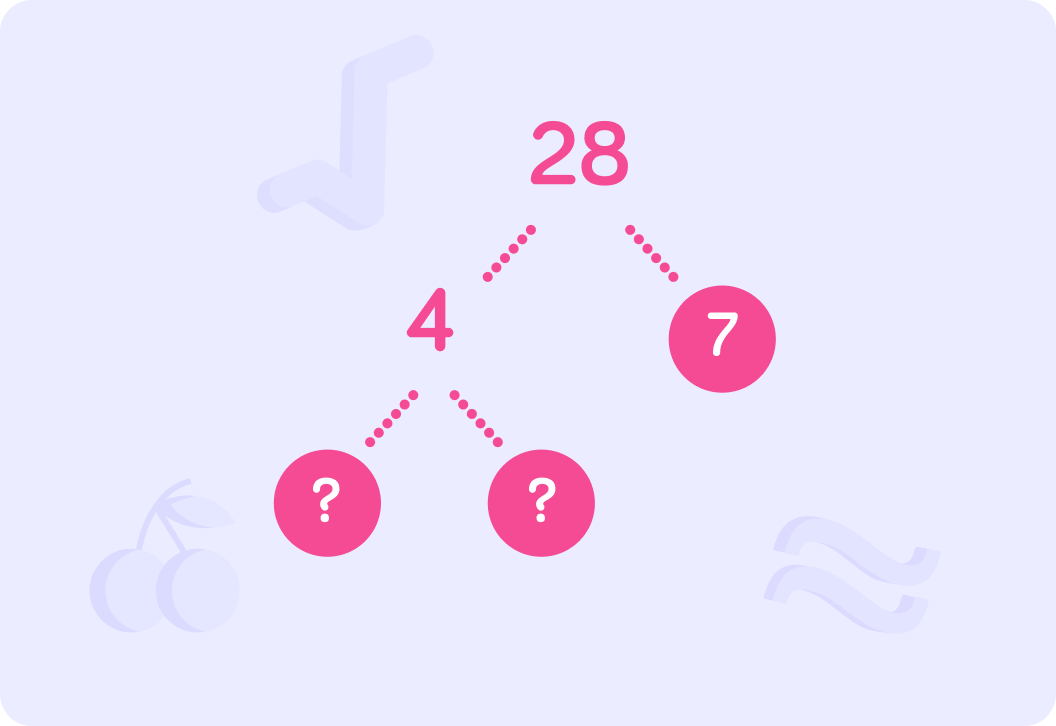
We have replaced the $?$ with the number $2$ .

We know that $2$ is prime so circle them both.

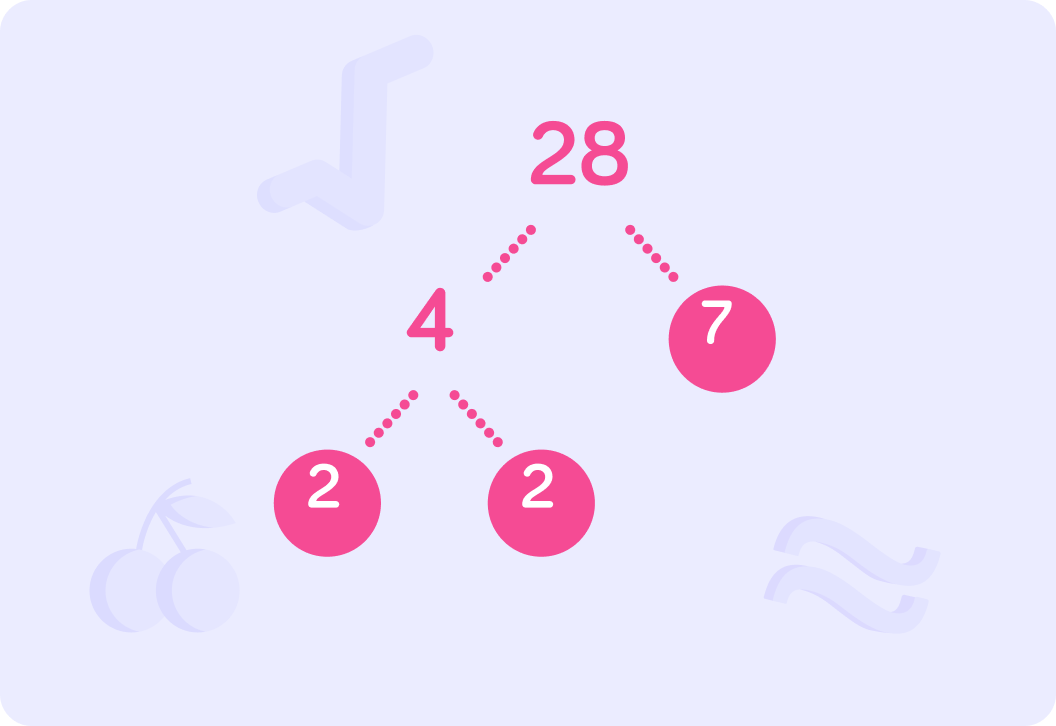
We now have the prime factorisation of the number $28$ .

Take the circled prime numbers and multiply them together: $2\times 2\times 7=28$

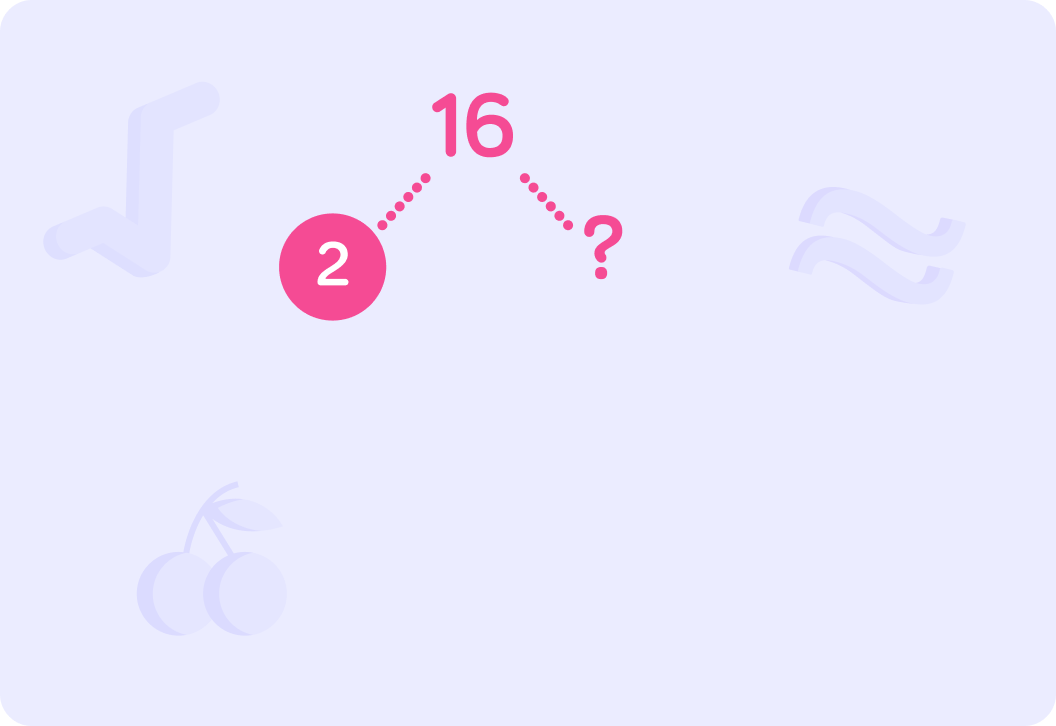
Let's find the prime factorisation of $16$ . If the first factor is $2$ , what number completes this stage of the tree?

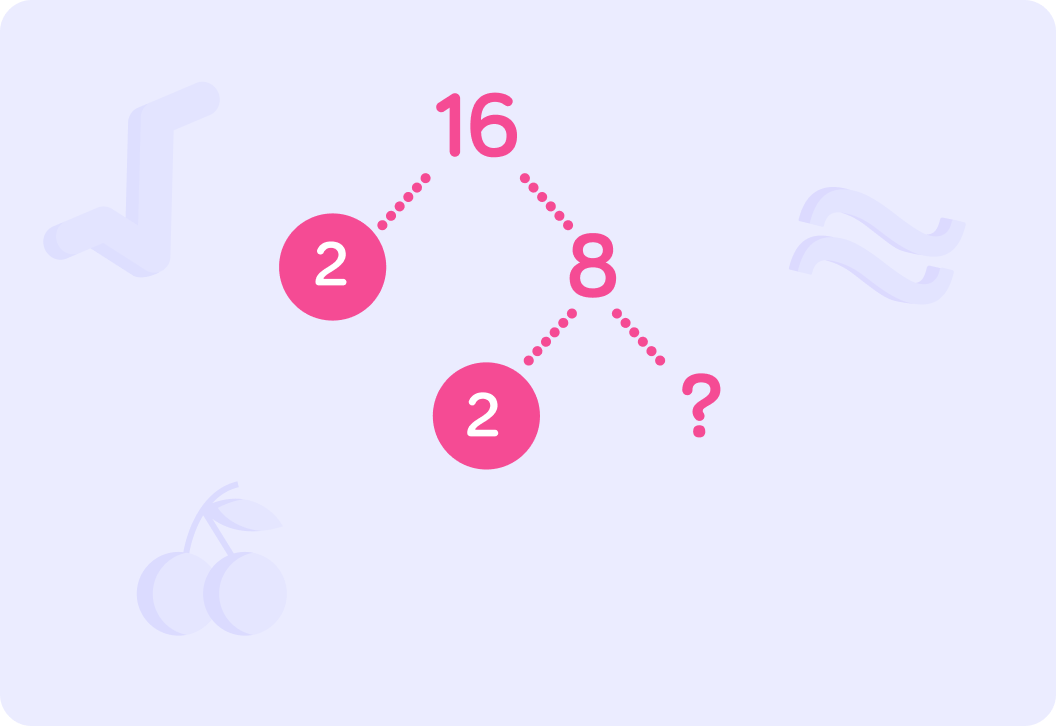
We've added $8$ which also has a factor of $2$ . What completes this stage of the tree?

Circle the prime numbers as you go. What number completes this tree?

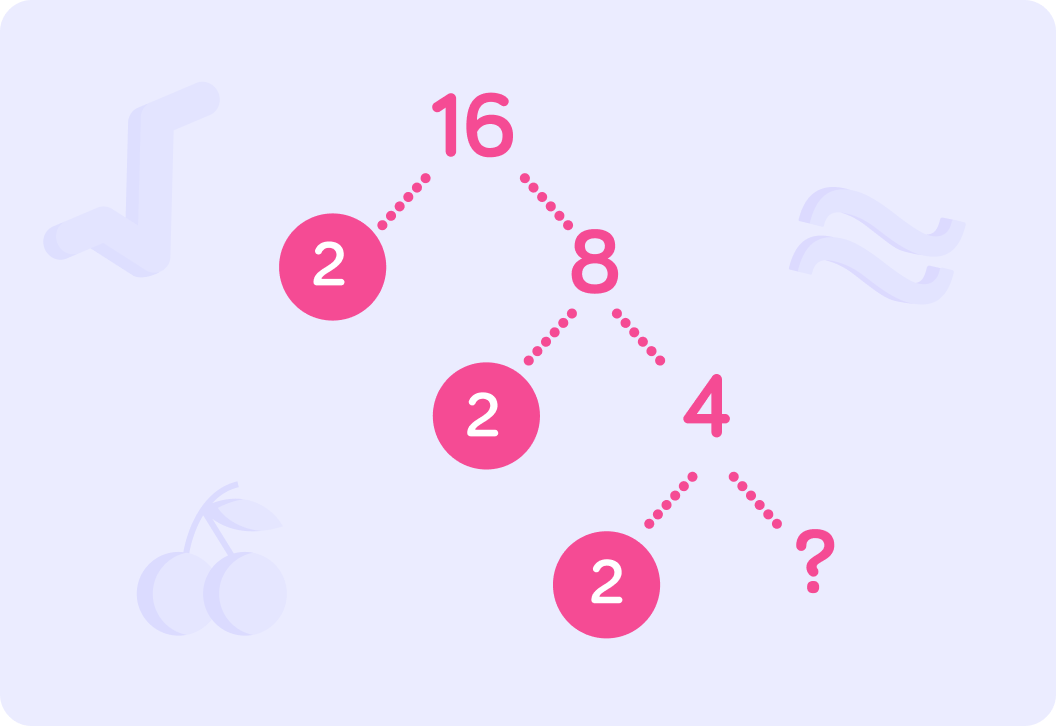
This is our completed tree for the prime factorisation of $16$ .

We bring this together by multiplying the prime factors so we have $2\times 2\times 2\times 2=16$ .

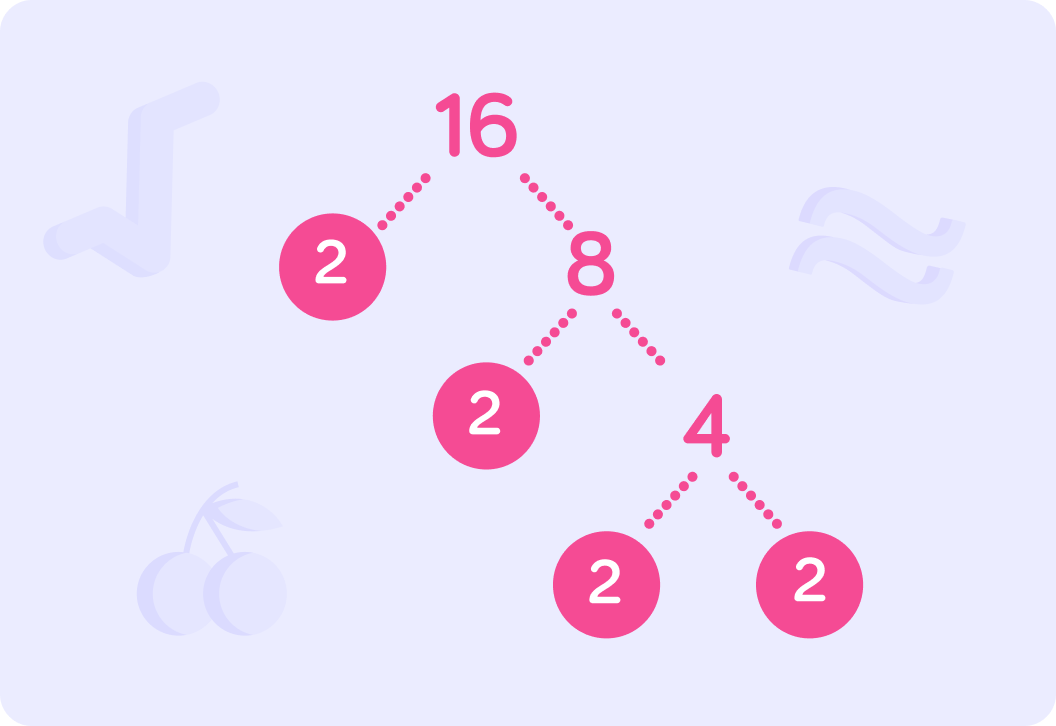
It's not the only way to draw a factor tree for $16$

Instead, we could start by splitting $16$ into $4 \times 4$ .

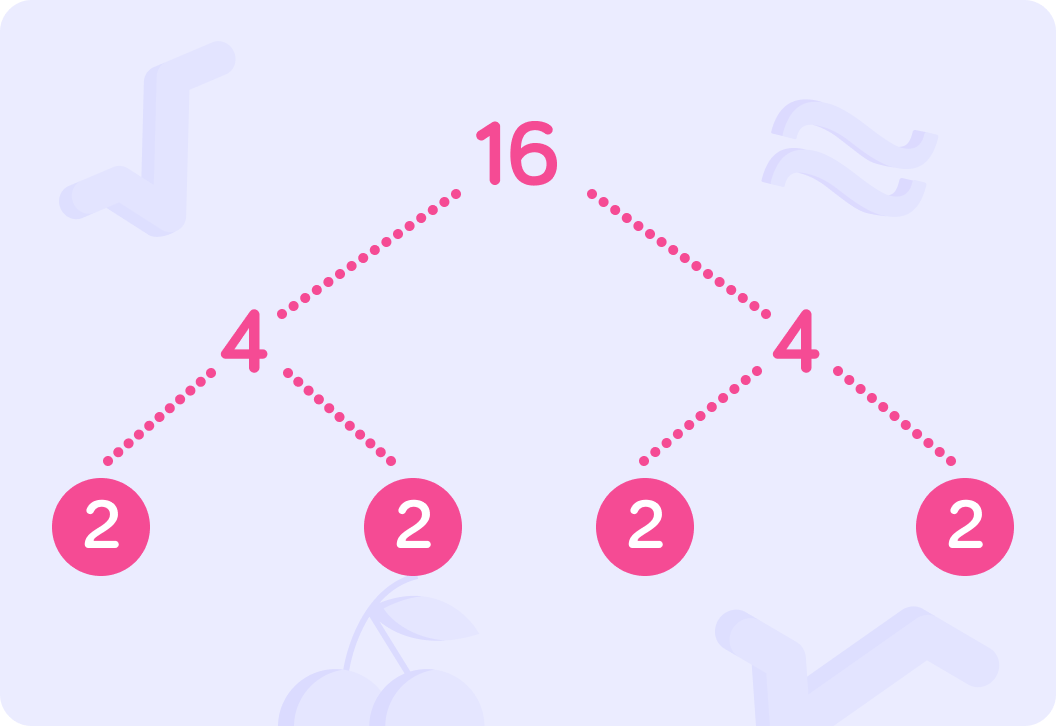
What's the prime factorisation now?

The two trees are different but the final answer is still the same.

Every composite number has a unique prime factorisation.

We have seen that the prime factorisation of $16$ is $2\times 2\times 2\times 2$ .

We can shorten this using the fact that powers of a number are repeated multiplication.

There are four $2s$ in the expression $2\times 2\times 2\times 2$ . Keeping $2$ as the base number, what is the power we need to use?

This gives an alternative way of writing the prime factorisation of $16$ .

$2^4=16$

Quick recap: what is prime factorisation and why is it helpful? Select all the options that apply.

You can select multiple answers

What is the prime factorisation of $36$ ? Take some time to work this out if you need to

We have seen that the prime factorisation of $36$ is $2\times 2\times 3\times 3$ . What is an alternative way of writing this?

Final question! Use prime factorisation to express $54$ as the product of its prime factors. Keep the factors in number order in your answer.

Summary!

A factor is a number which divides exactly into another number with no remainder or decimal answer.

$4$ is a factor of $12$ as $12\div 4=3$

$5$ is not a factor of $12$ as $12\div 5=2.4$

A prime factor is a factor that is a prime number.

$4$ is a factor of $12$ but it is not a prime factor

$3$ is a prime factor of $12$

Every number has a unique prime factorisation

The prime factorisation of $12$ is $2\times 2\times 3$ or $2^2\times 3$ .

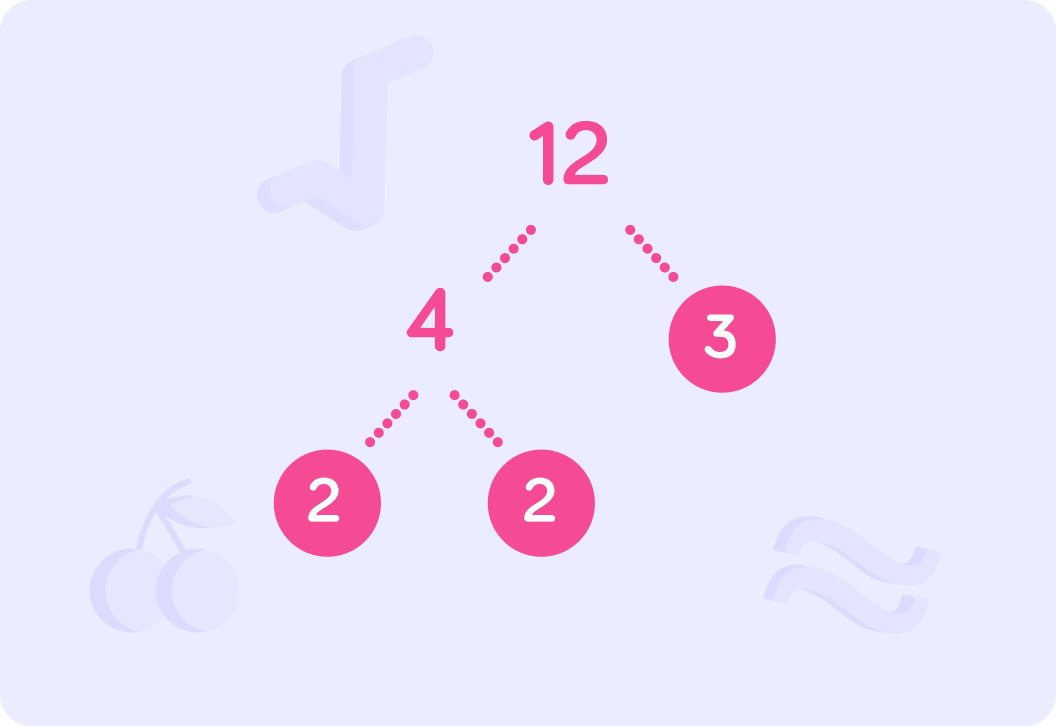
Use a prime factor tree to find the prime factorisation of a number.

Prime factorisation of $28$ is $2\times 2\times 7$ or $2^{2}\times7$