Number

YOU ARE LEARNING:

Lowest Common Multiples

Lowest Common Multiples

The lowest common multiple is the smallest number that is a multiple of two other numbers.

A multiple is a number that is a product of two numbers. Which number below is a multiple of $5$ ?

So $135$ is a multiple of $5$ because $5\times 27=135$ .

It's also true that $135=15\times 9$ .

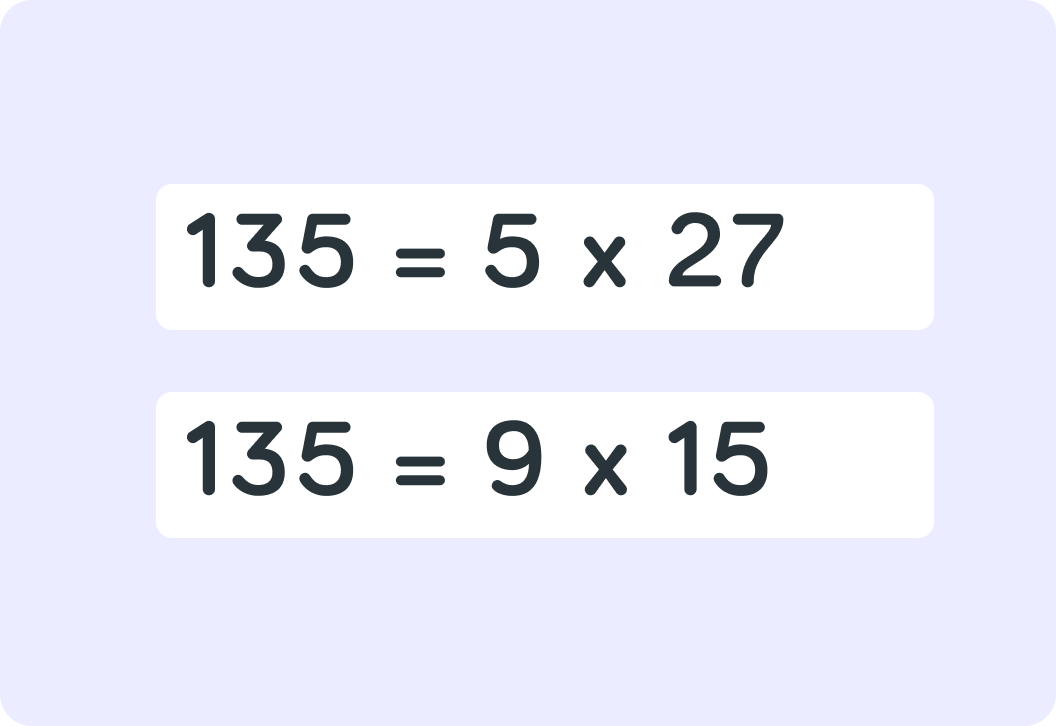
This means that $135$ is a multiple of $5$ and $15$ . What is the term for this?

Sometimes we want to find the lowest common multiple of two numbers.

This is the smallest number that is a common multiple of them both. There are two ways we can approach this.

Let's find the lowest common multiple (LCM for short) of $8$ and $6$ .

List the first three multiples of $8$ separating your answers with a comma.

Are any of these also a multiple of $6$ and if so, which one?

We have found the lowest common multiple of $6$ and $8$ .

The LCM is $24$ .

Let's find the LCM of $12$ and $15$ .

We list the multiples of the larger number - this means we have fewer multiples to find!

What are the first three multiples of $15$ ? Separate your answers with a comma.

The first three multiples of $15$ are $15$ , $30$ and $45$ . Are any of these also a multiple of $12$ ?

We need to find more multiples of $15$ . The first three are $15$ , $30$ and $45$ . What are the next three? Separate your answers with a comma.

The next three multiples of $15$ are $60$ , $75$ and $90$ . Are any of these also a multiple of $12$ and if so which one?

We have found the LCM of $12$ and $15$ which is $60$ .

Sometimes we have to find quite a few multiples, there is another method which can be quicker.

What is the LCM of $12$ and $15$ using prime factorisation?

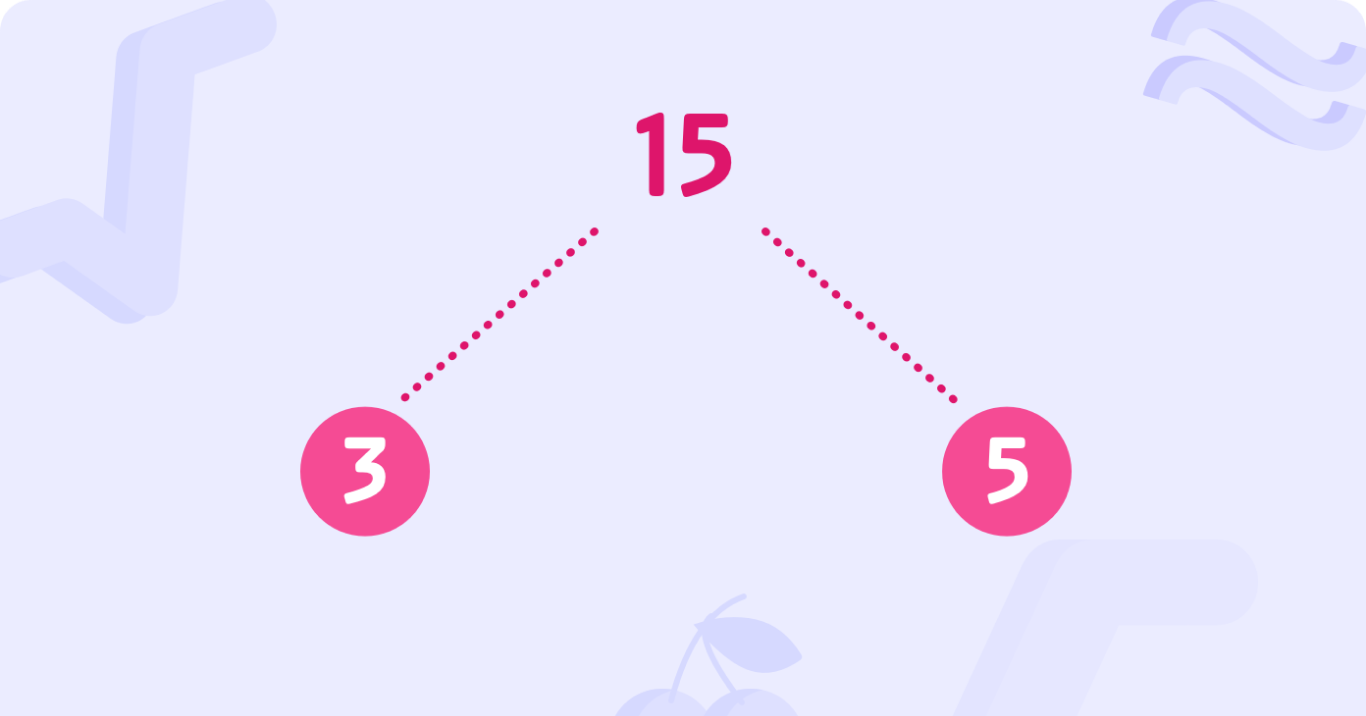
This is the prime factorisation of $15$

$3$ and $5$ are both prime numbers that multiply to make $15$ .

What is the prime factorisation of $12$ ?

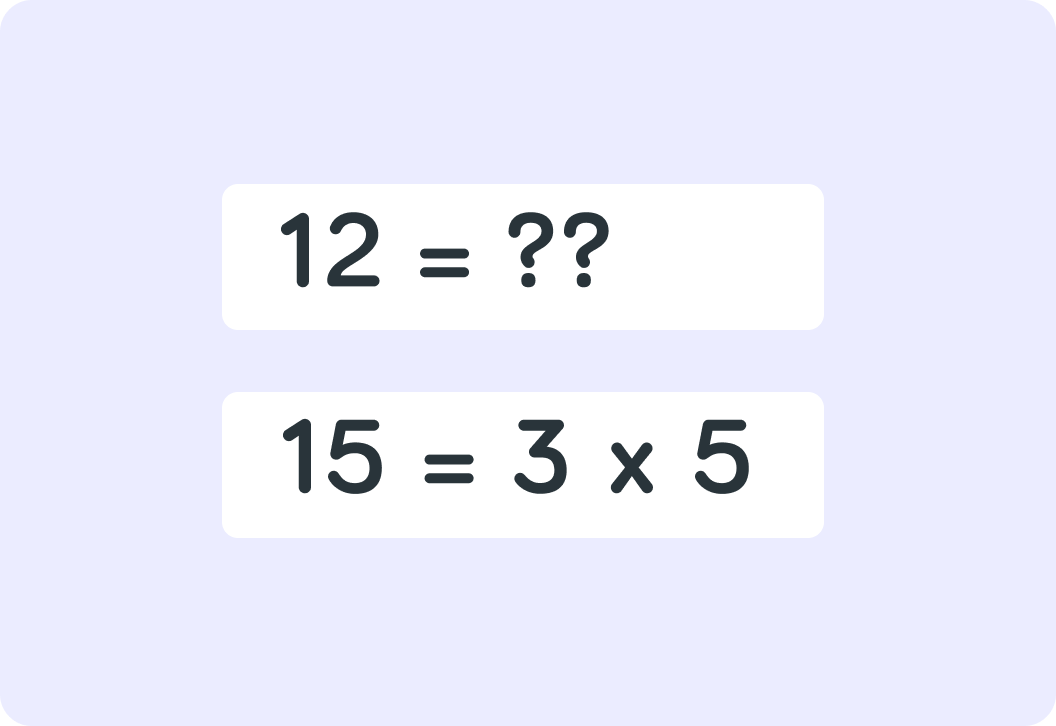
We have the prime factorisation of both our numbers.

To find the LCM we eliminate the duplicate of any common prime factors the multiply the numbers that remain

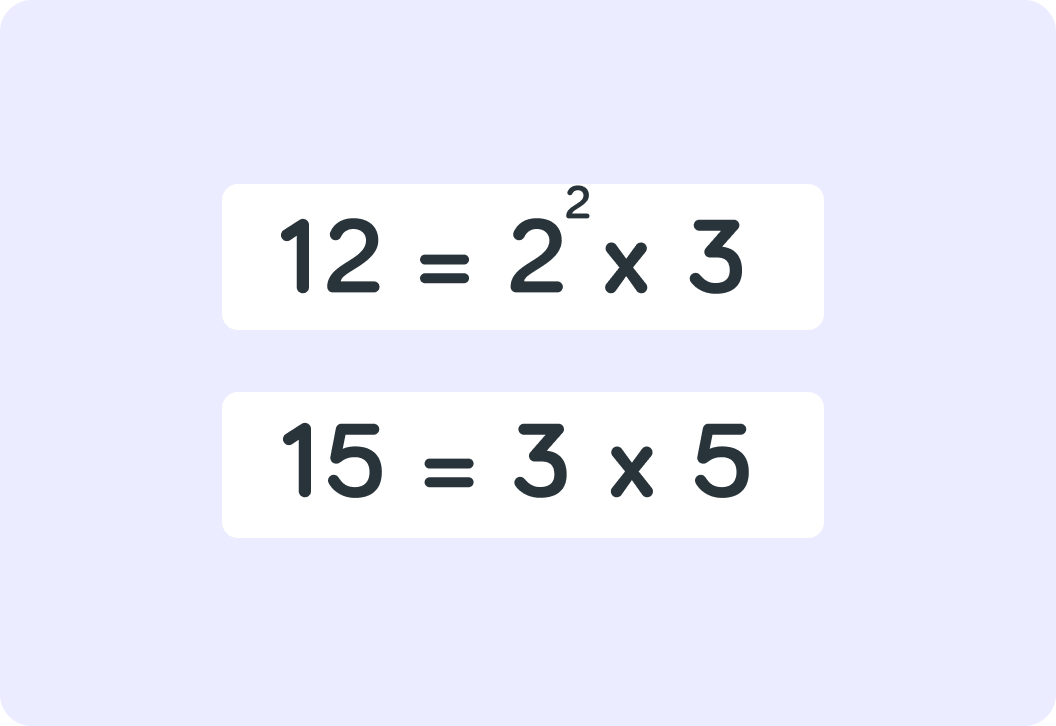
Which prime factors do each of these numbers have in common?

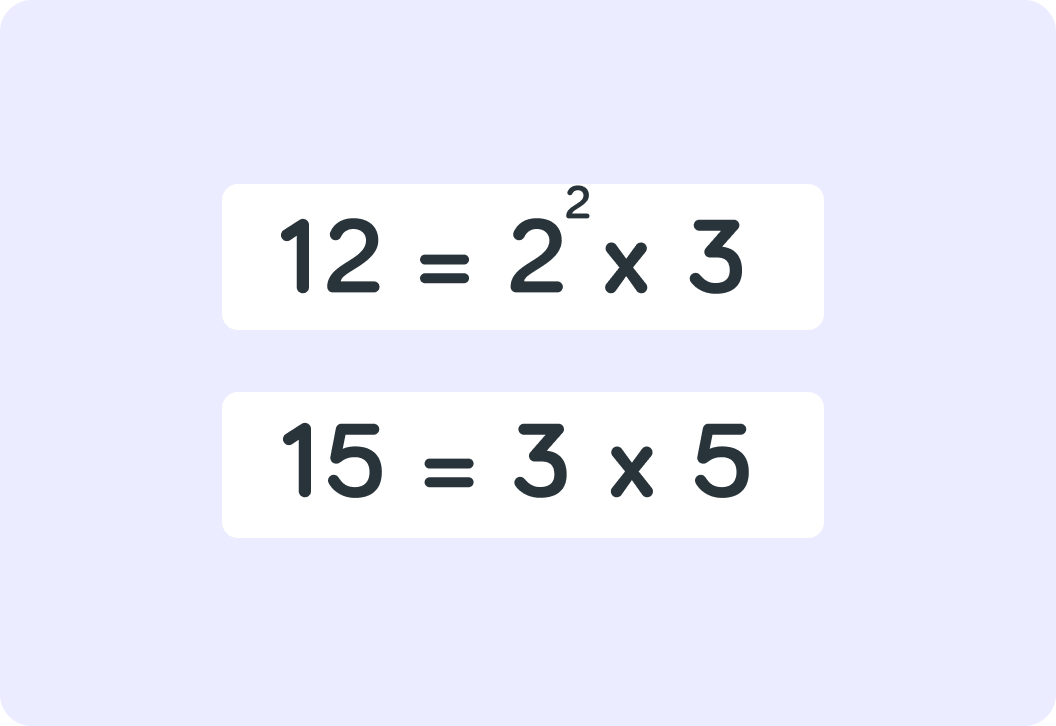
We eliminate one of these common factors so that we don't duplicate it. Are there any other common prime factors?

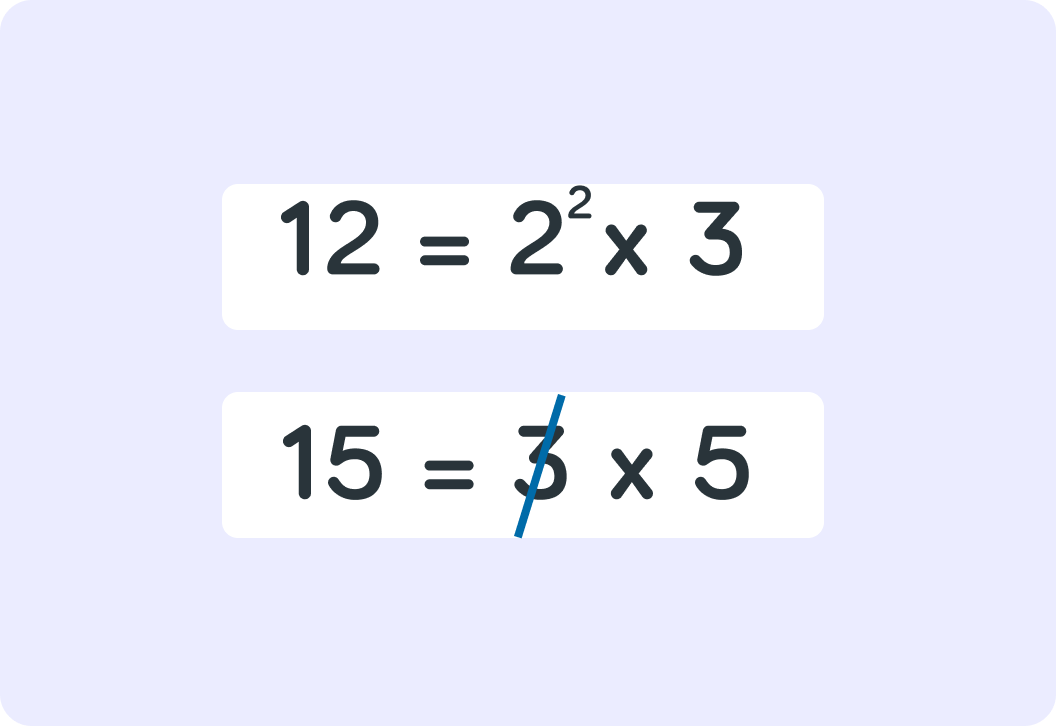
To find the LCM, we take the remaining prime factors and multiply them all together. What is the answer?

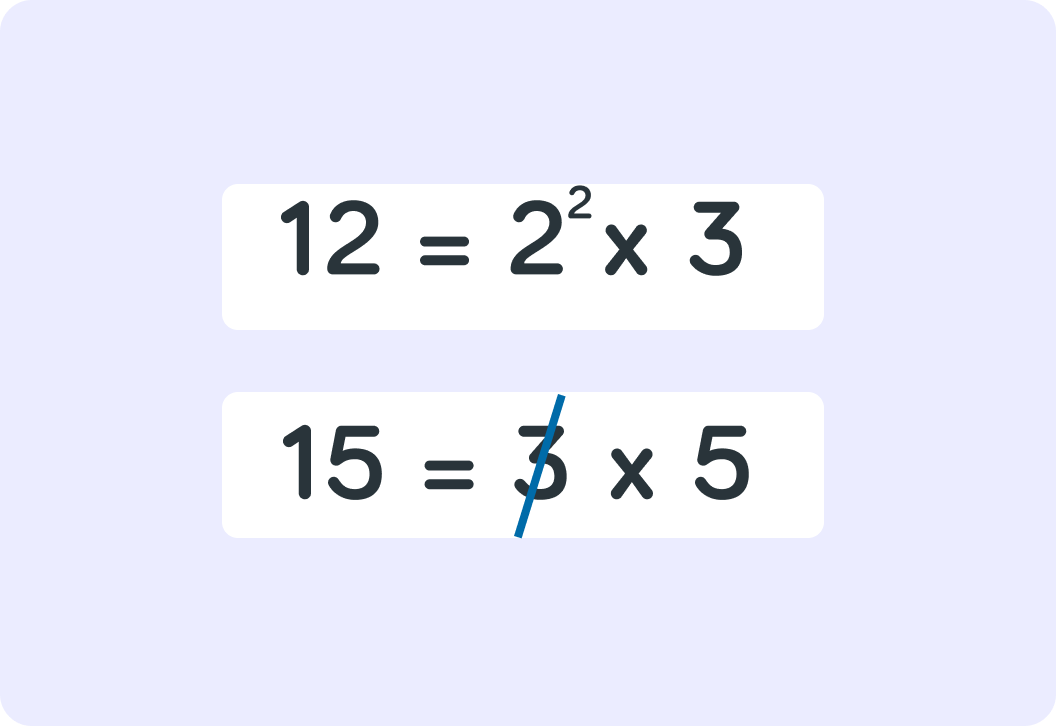
We have used both methods to find the LCM of $12$ and $15$ is $60$

Prime factorisation means we don't need to find lots of multiples.

Let's work through this one - find the LCM of $40$ and $90$ .

The prime factorisation of $90$ is $2\times 3^2\times 5$ .

What is the prime factorisation of $40$ ?

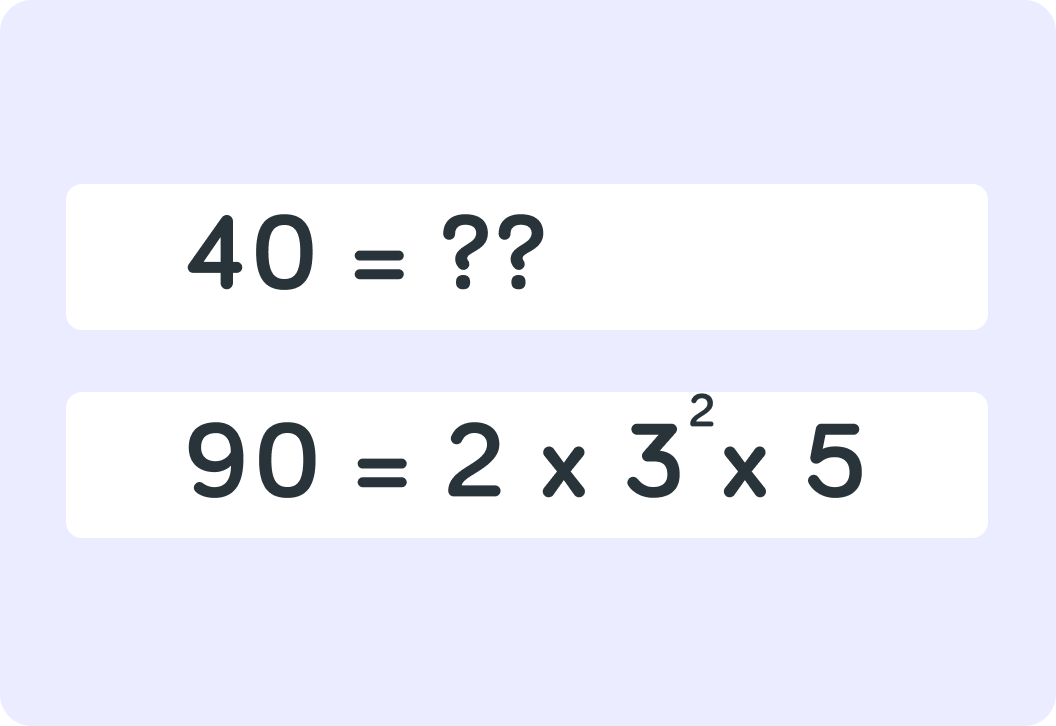
We now have the prime factorstions of both numbers. What are the common prime factors? Separate your answer with a comma.

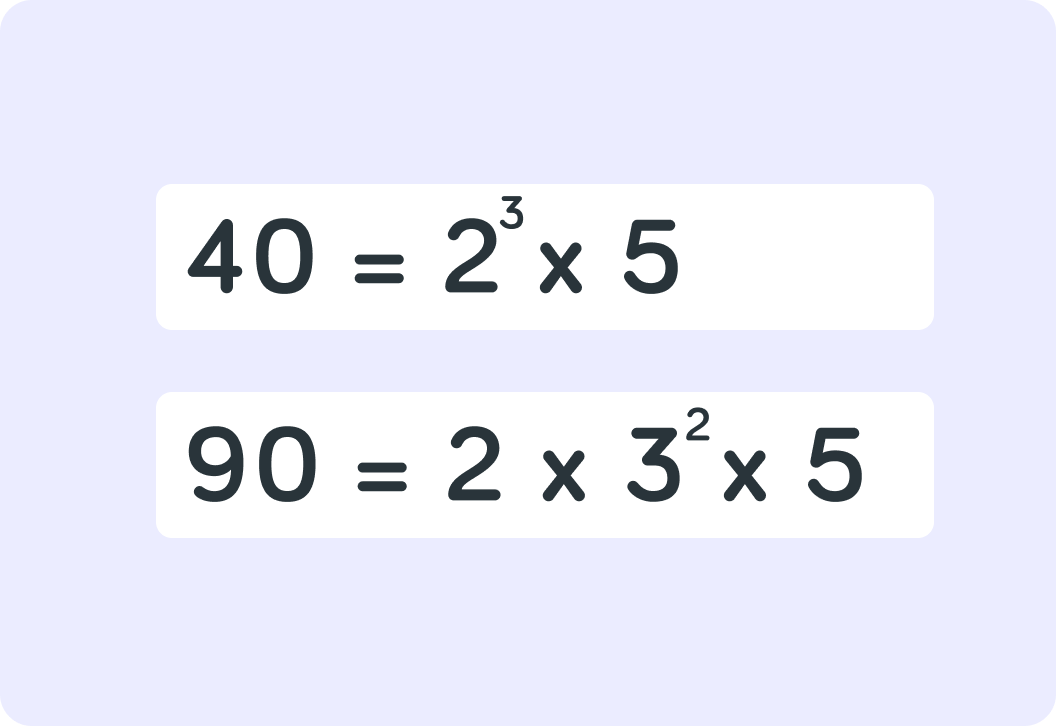
This time we need to be careful which prime factor we cross through.

Where a factor has a power, we cross through the factor with the lowest power.

Find the LCM of $40$ and $90$ by multiplying out the remaining prime factors.

Well done - you've found the LCM of $40$ and $90$ !

The LCM is $360$ .

Let's find the LCM of $16$ and $40$ . First find the prime factorisation of $16$ .

Now find the prime factorisation of $40$ .

The prime factorisations are: $16=2^4$

$40=2^3\times 5$ Which is the only common prime factor?

The prime factorisations are: $16=2^4$

$40=2^3\times 5$ Taking out the duplicate factors, what is the LCM of $16$ and $40$ ?

Use either method to find the Lowest Common Multiple of $14$ and $8$ .

What is the LCM of $75$ and $90$

Summary!

A multiple is a number that is a product of two numbers.

$20$ is a multiple of $5$ because $5\times 4=20$ .

A common multiple is a number that is a multiple of two other numbers.

$20$ is a common multiple of $5$ and $10$ .

There are two ways of finding the LCM of two numbers

List the multiples of the larger number and stop when you find a multiple of the smaller number.
Use the prime factorisation technique

List multiples of $15$ to find the LCM of $6$ and $15$

Find multiples of $15$ until you reach a multiple of $6$ . These are $15$ , $30$ and we stop there because $30$ is also a multiple of $6$ .

Prime factorisation can also be used to find the LCM.

The LCM of $15$ and $27$ is $135$ .

The prime factorisation of: $15=3\times 5$

$27=3^3$

Cross through the common prime factors, where there is a power, cross through the lowest power. This leaves ${\cancel{3}}\times 5$ and $3^3$ giving the LCM as $3^3\times 5=135$ .