Number

YOU ARE LEARNING:

Indices: Higher Powers

Higher powers make numbers bigger very very quickly!

The index number $5^2$ is the same as_____

The index number $7^3$ is the same as______

Using the same principle as square and cube numbers, what is $2^5$ the same as?

What is $4^6$ the same as in the form $x \times x \times x...$ ?

Index numbers like $5^7$ are made up of a base number and a power. Which number is the power?

In the index number $5^7$ :

The base number is $5$ The power is $7$

What is the base in the expression $a^n$ ?

Sometimes the power is also called the index.

In $a^n$ we can say $n$ is the power or the index.

Increasing powers makes numbers higher very very quickly!

For example, $5^1$ is just $5$ , while $5^5$ is $3,125$

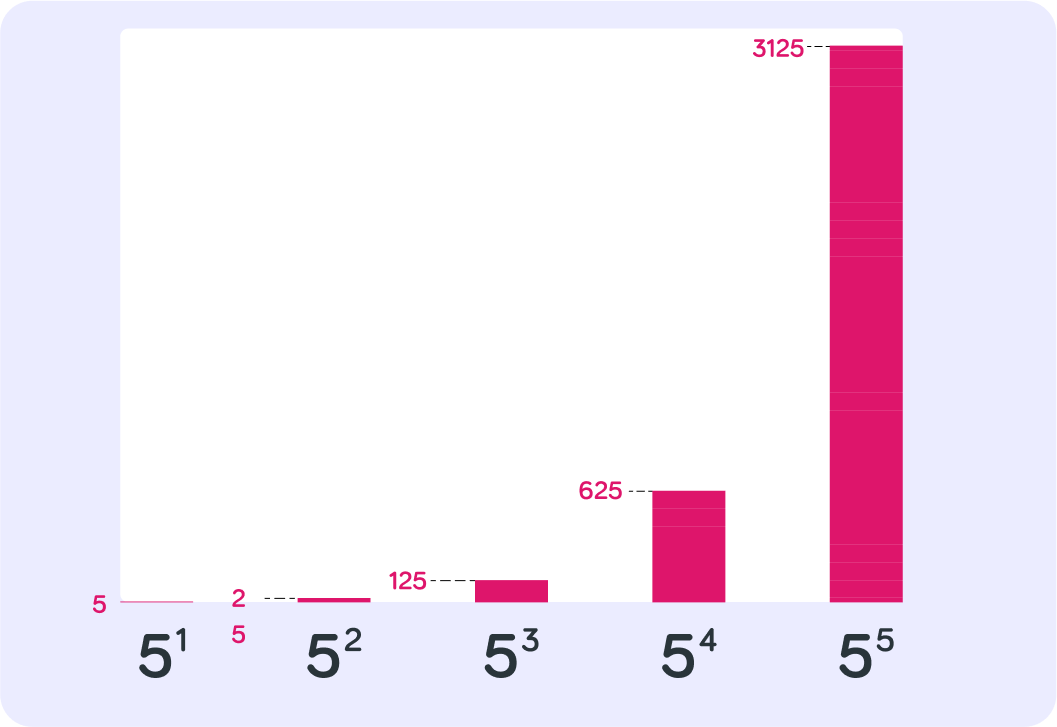
When numbers get very big very quickly like this

it is known as exponential growth.

What does $3^4$ actually equal?

What does $2^5$ equal?

A useful power to know is the power $1$ . What do you think $2^1$ equals?

Now find $12^1$ .

From this we can see that any number raised to the power $1$ is itself.

$x^1=x$

Summary!

Powers tell you how many times you should multiply the number by itself

For example $4^6$ is the same as $4$ multiplied by itself 6 times.

$4 \times 4 \times 4 \times 4 \times 4 \times 4$

Any number raised to the power $1$ is itself.

$x^1=x$

In the expression $x^y$

$x$ is the base number $y$ is the power

Increasing powers makes numbers higher very very quickly!

For example, $3^1$ is just $3$ , while $3^8$ is $6,561$