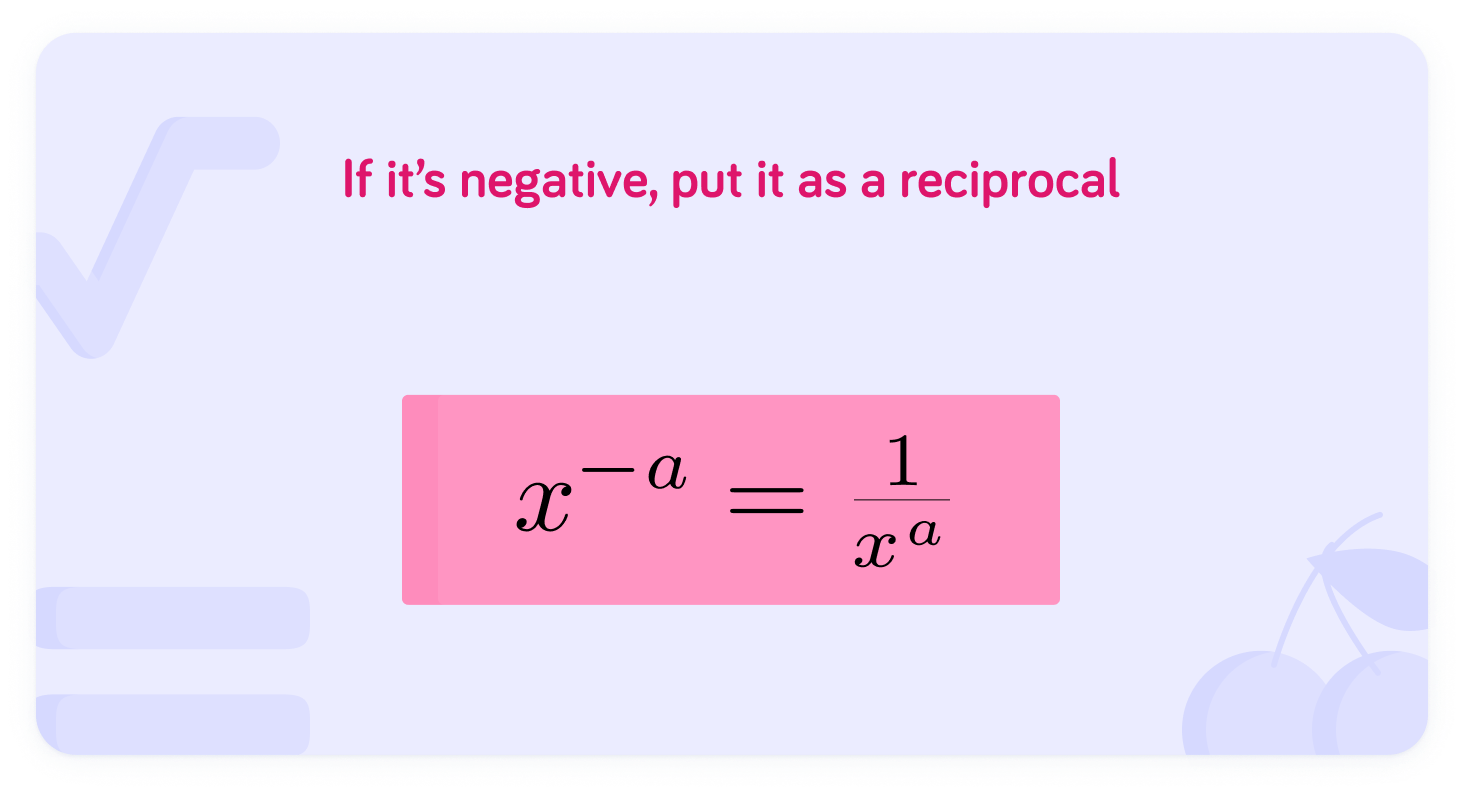Number

YOU ARE LEARNING:

Indices: Negative Powers

Raising a number to a negative power creates a reciprocal: a fraction where 1 is the denominator.

The power in an index number can be negative like $3^{-2}$ or $4^{-5}$

To see how this works, we need to divide some index numbers.

What is $\dfrac{x^3}{x^5}$ ?

We have found that $\dfrac{x^3}{x^5}=x^{-2}$ , an answer which has a negative power.

But what does $x^{-2}$ mean?

We found that $\dfrac{x^3}{x^5}=x^{-2}$ .

Let's expand our calculation to understand the answer.

What is another way of writing $x^3$ ?

We can write $x^5=x\times x\times x\times x\times x$

This gives $\dfrac{x^3}{x^5}=\dfrac{x\times x\times x}{x\times x\times x\times x\times x}$ .

We can now cancel the $x$ pairs in the numerator and denominator.

$\dfrac{{\cancel{x}}\times {\cancel{x}}\times {\cancel{x}}}{{\cancel{x}}\times {\cancel{x}}\times {\cancel{x}}\times x\times x}$

Now we have cancelled the $x$ terms, how is this simplified? $\dfrac{{\cancel{x}}\times {\cancel{x}}\times {\cancel{x}}}{{\cancel{x}}\times {\cancel{x}}\times {\cancel{x}}\times x\times x}$

By breaking the fraction down we have shown that

$\dfrac{x^3}{x^5}=\dfrac{1}{x^2}$

We have seen that $\dfrac{x^3}{x^5}=x^{-2}$ and $\dfrac{x^3}{x^5}=\dfrac{1}{x^2}$ , what does that mean?

This is the rule for negative powers

$x^{-2}=\dfrac{1}{x^2}$

We have found the rule for negative powers, $x^{-2}=\dfrac{1}{x^2}$ . How can we state this in words?

A reciprocal is one over the original number.

The reciprocal of $2$ is $\dfrac{1}{2}$ .

If the power is negative, express it as a reciprocal

Have a look at the image

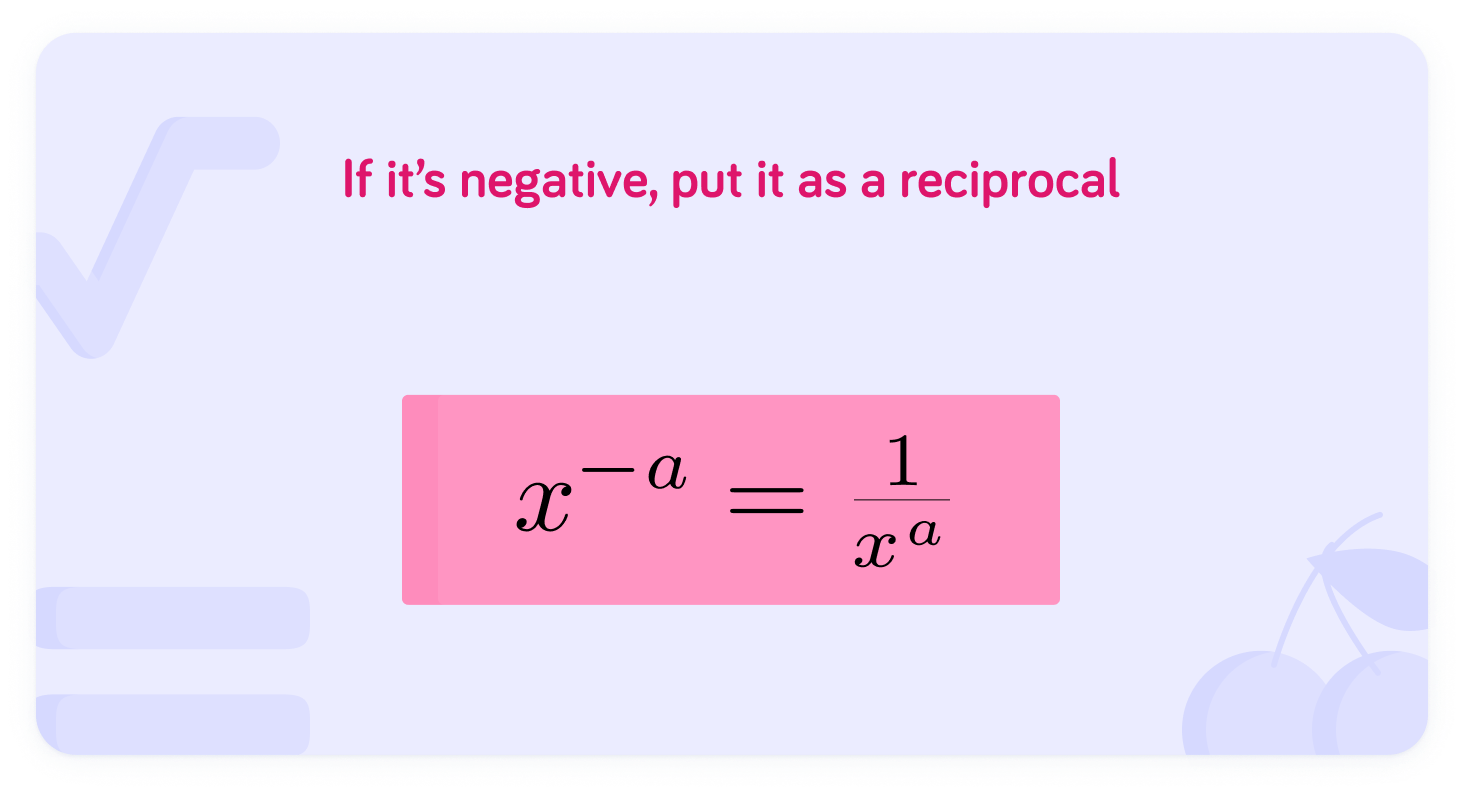
Let's try this one $8^{-2}$ .

First we take out the negative sign to give $8^2$ .

First, what is the reciprocal of $8^2$ ?

Finally, we calculate the denominator to give

$8^{-2}=\dfrac{1}{64}$ .

What is $6^{-1}$ ?

Let's have a go at an example: $3^{-3}$

Remove the negative sign

This will leave us with the index $3^3$ .

Find the reciprocal of $3^3$ .

So far we have $3^{-3}=\dfrac{1}{3^3}$ , what is the final answer?

Our final fractions is

$\dfrac{1}{27}$ Nice 👍

Try this one: what is $4^{-3}$ ?

What is $5^{-2}$ ?

Summary! A reciprocal is one over the original number

The reciprocal of $2$ is $\dfrac{1}{2}$ .

Indices or powers can be negative numbers

$x^{-y}$ is an index number with a negative power.

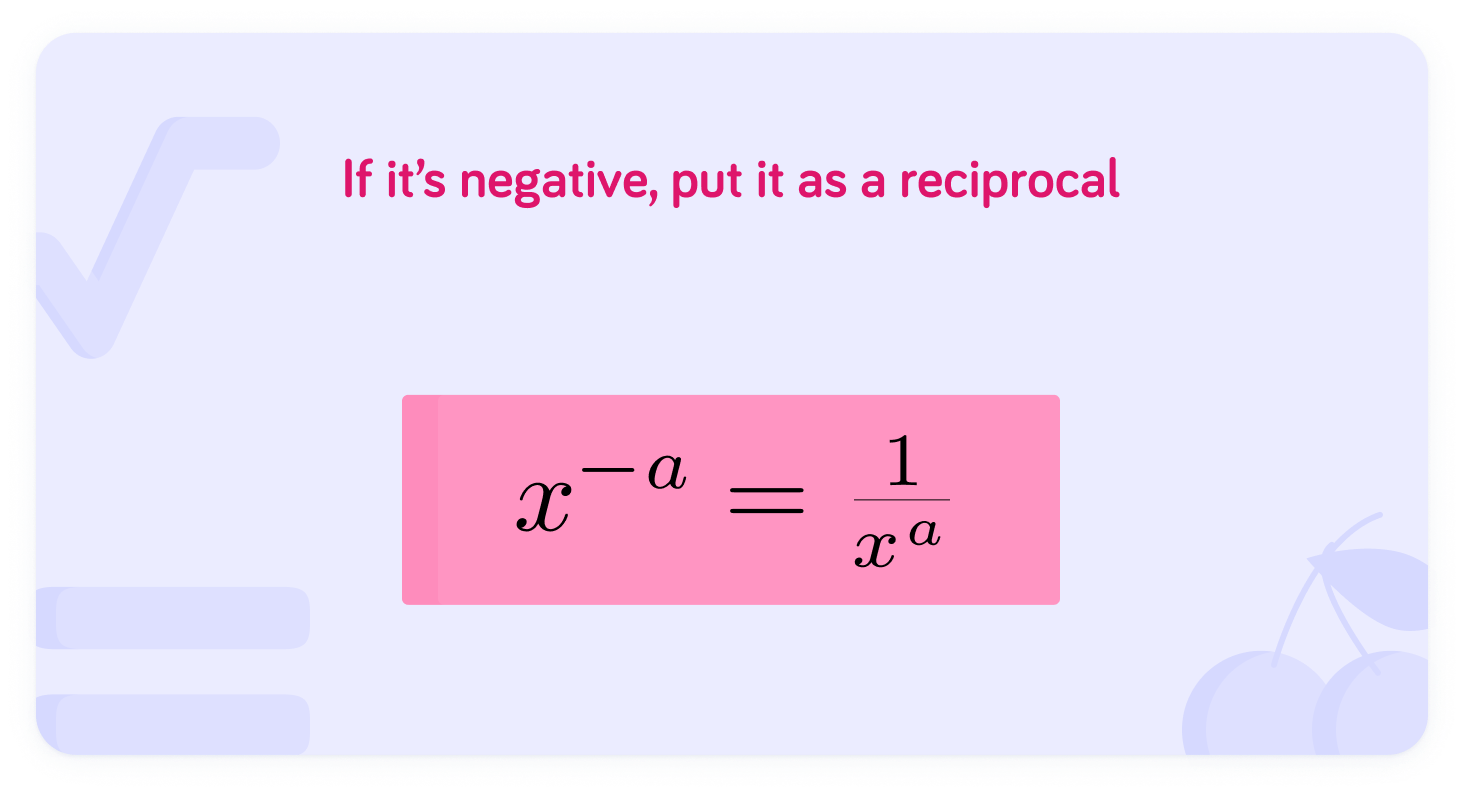
A negative power is the reciprocal of the positive power

The image shows how that works

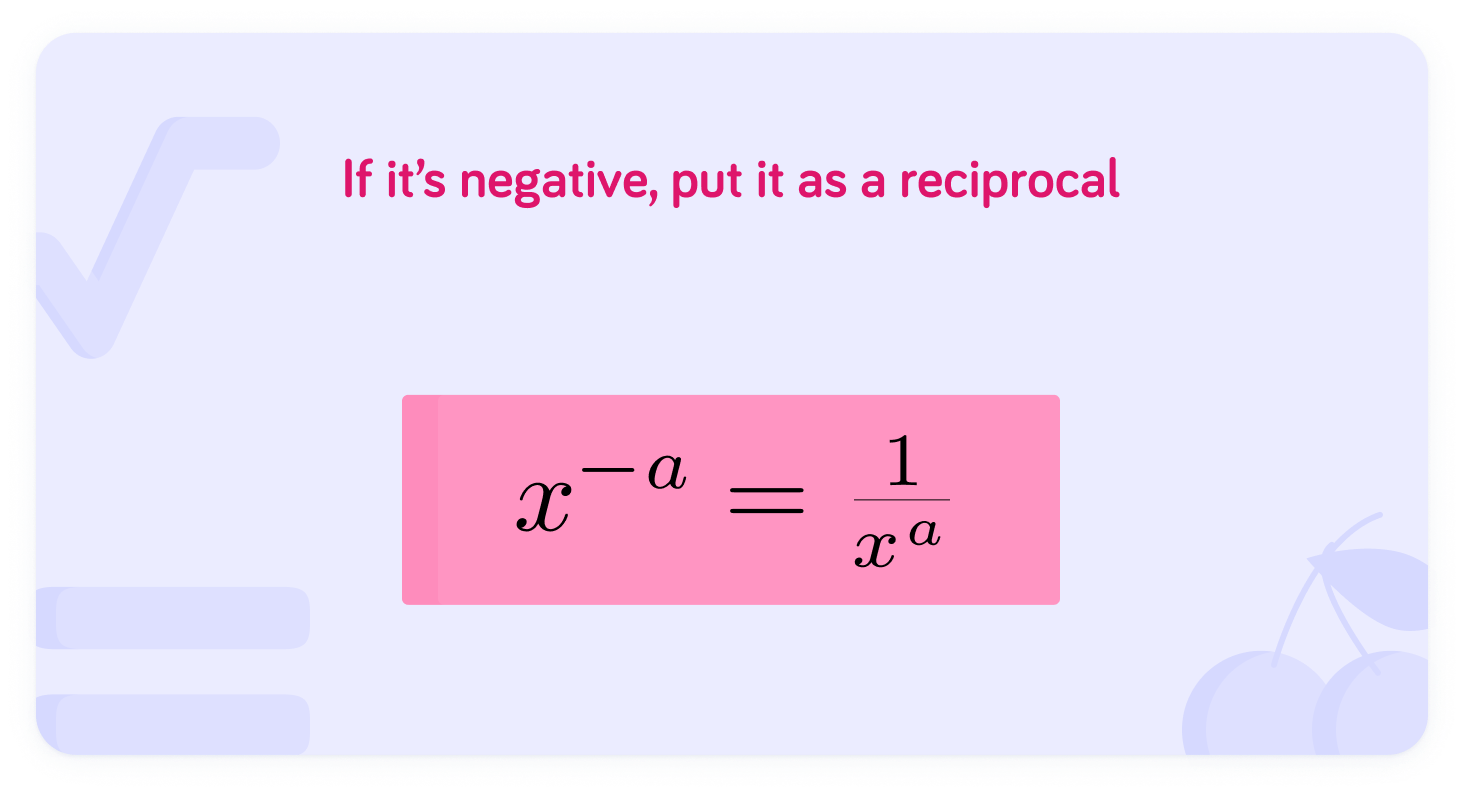
We can find $2^{-2}$

First we have $2^{-2}=\dfrac{1}{2^2}$

We simplify to $\dfrac{1}{2^2}=\dfrac{1}{4}=0.25$