Number

YOU ARE LEARNING:

Indices: Squares and Cubes

You can multiply a number by itself infinite times, where the number of multiplications is called the power. The most common powers are called squares and cubes.

To get started, what is this shape?

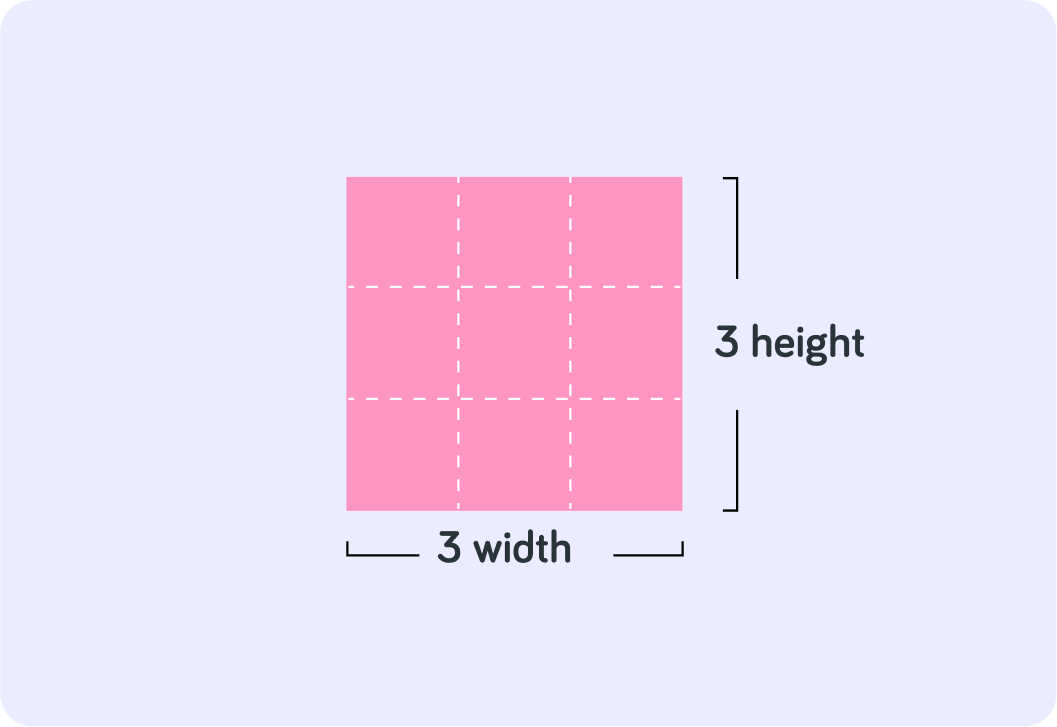
And would you calculate the area of this square?

True or false? The width and the height will always be the same length in a square.

You can also write $3 \times 3$ as $3^2$

You read $3^2$ as "3 to the power of 2" or "3 squared", because it equals the area of a square whose sides are length $3$

So $3 \times 3$ and $3^2$ (3 squared) is the same. What does $3^2$ equal?

The area of the square, whose sides are length $3$ , equals $9$

So $3 \times 3$ or $3^2$ (3 squared) equals $9$

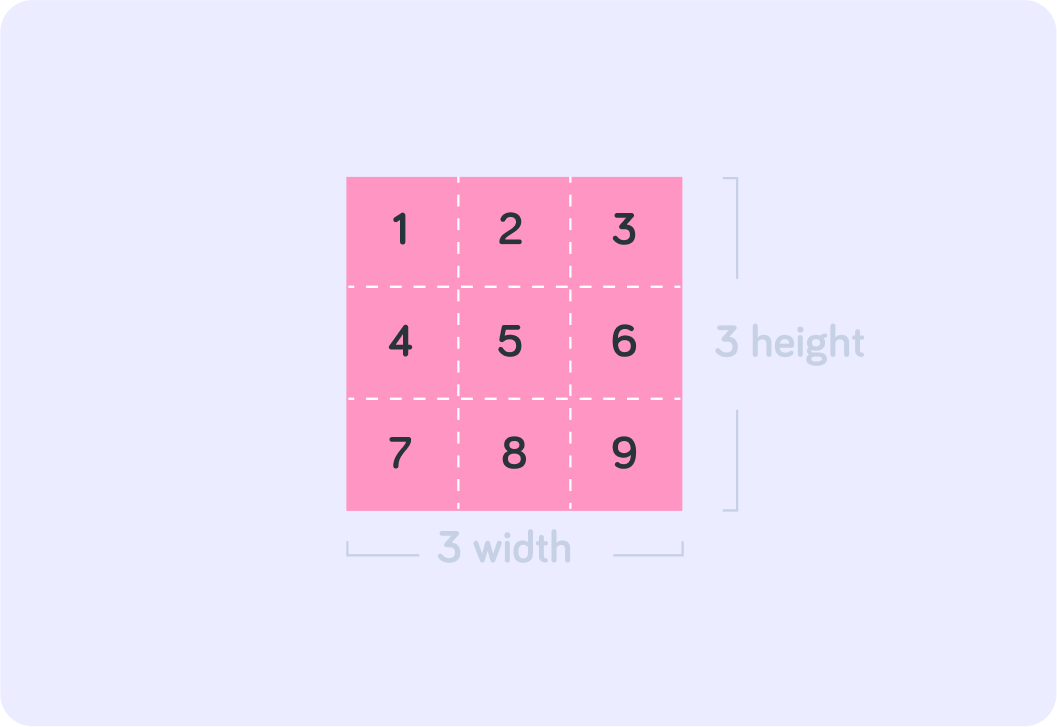
The little $^2$ in $4^2$ is called the power

You can also say "4 to the power of 2". Numbers that are raised to powers, like $4^2$ , are called indices. Sometimes, the power is also called the index.

What does $4^2$ (4 squared) equal?

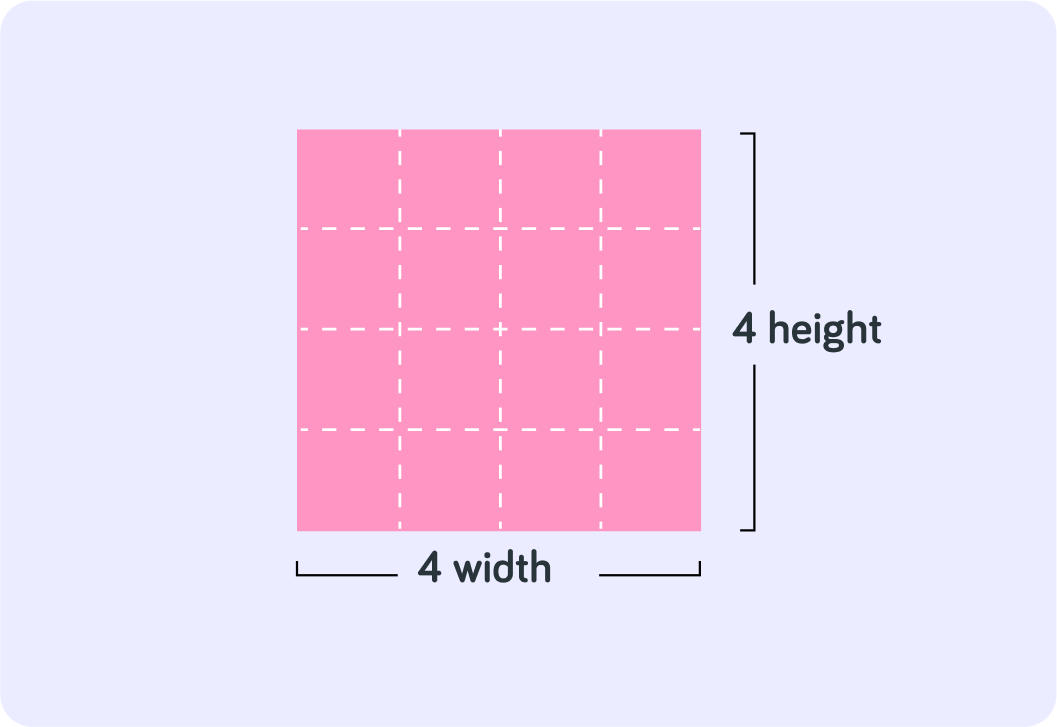
What does $1^2$ (one squared) equal?

What does $5^2$ (5 squared) equal?

Now what is this shape?

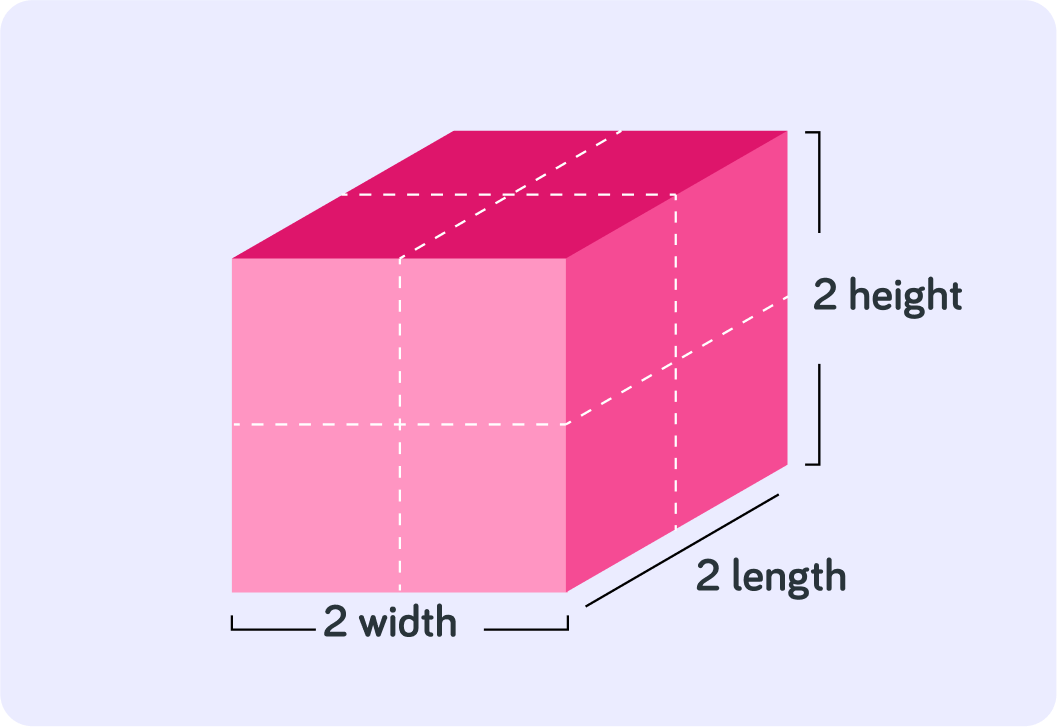
How do you calculate the volume of this cube?

So you would calculate the volume of this cube like $2 \times 2 \times 2$ . How do you think you can also write that?

You can also read $2^3$ as "2 __________".

$2^3$ essentially represents the volume of a cube

So you can read $2^3$ as "2 cubed".

What does $3^3$ (3 cubed) equal?

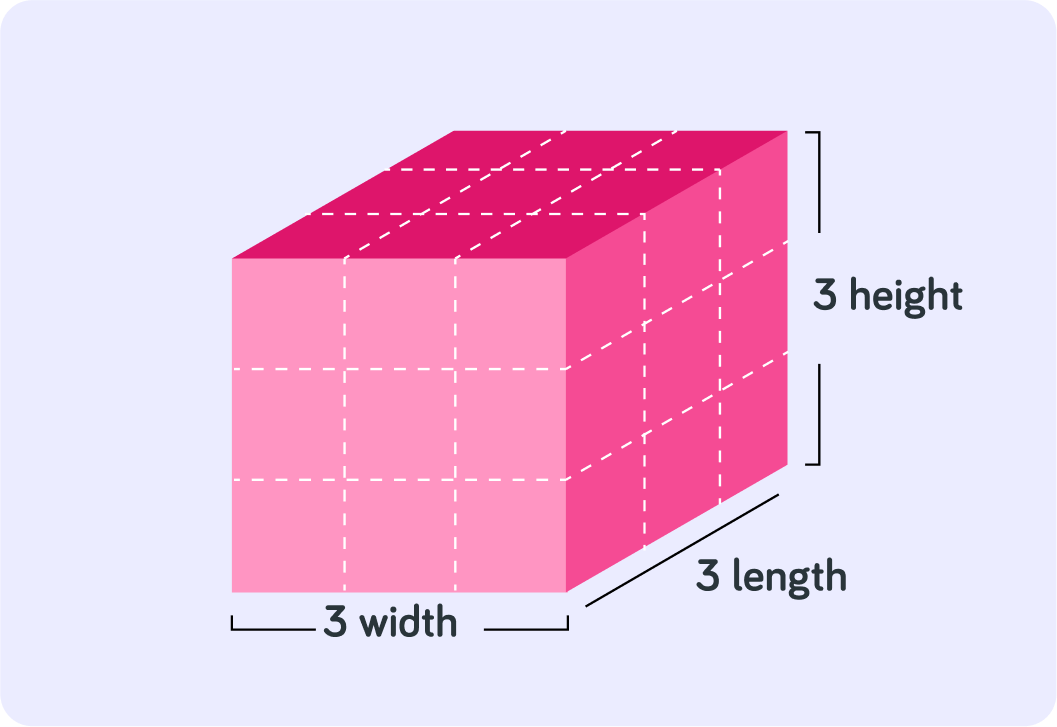
What does $1^3$ (1 cubed) equal?

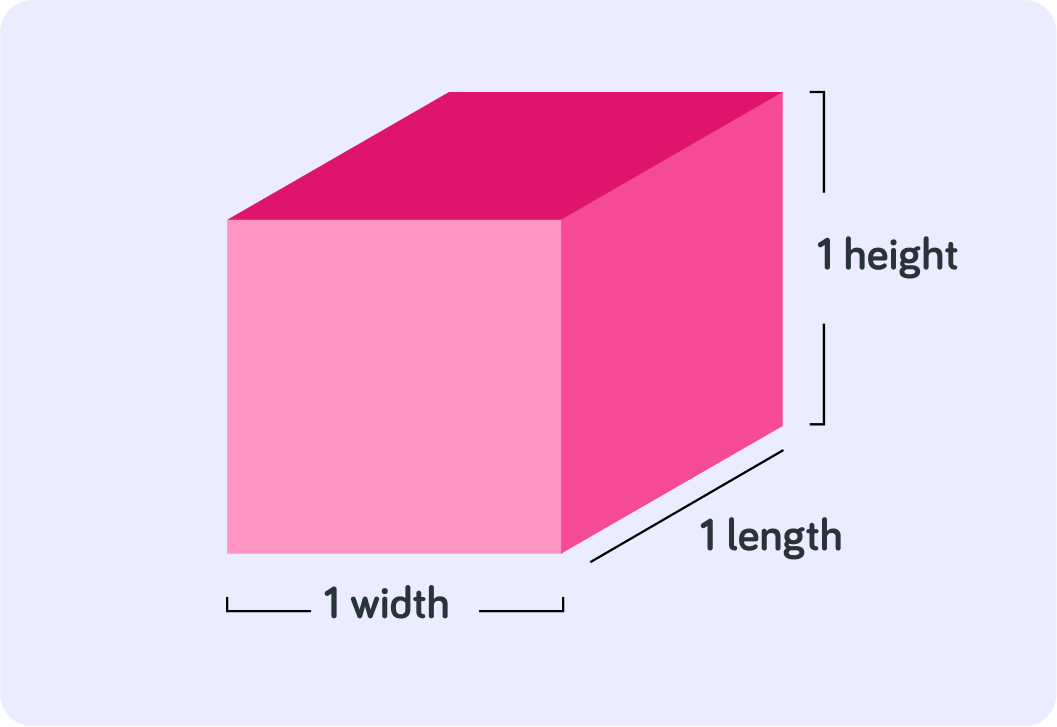
What does $5^3$ (5 cubed) equal?

What does $4^3$ (4 cubed) equal?

Summary! You can "square" a number

This means you multiply it by itself, like when you find the area of a square.

For example $3^2$ (3 squared) equals $9$

This is because $3 \times 3=9$

You can also "cube" a number

This means you multiply it by itself 3 times, like when you find the volume of a cube.

For example $3^3$ (3 cubed) equals $27$

This is because $3 \times 3 \times 3=27$

Numbers like $4^2$ or $5^3$ are called indices

You say "one index" and "many indices".

The little $^2$ in $4^2$ and the little $^3$ in $5^3$ are called powers or indices.

You can also say "4 to the power of 2" and "5 to the power of 3".