Albert Teen

powered by

GCSE Exam Guide Parent

>

>

Probability and statistics

>

Probability & Statistics

YOU ARE LEARNING:

Histograms

Histograms

Histograms

A histogram plots data where grouped intervals are not equal in size.

When data is collected in grouped intervals, the intervals may not be equally sized. When plotted as a bar chart, the bars are therefore different sizes. This is called a histogram.

In a histogram, the area of each bar represents the frequency, and frequency is not plotted on the y-axis. Instead, we plot “frequency density” on the y-axis.

1

The table shows the amount of money spent by a group of people on a weekend

To draw a histogram, we need to add two additional columns: the class width and the frequency density.

2

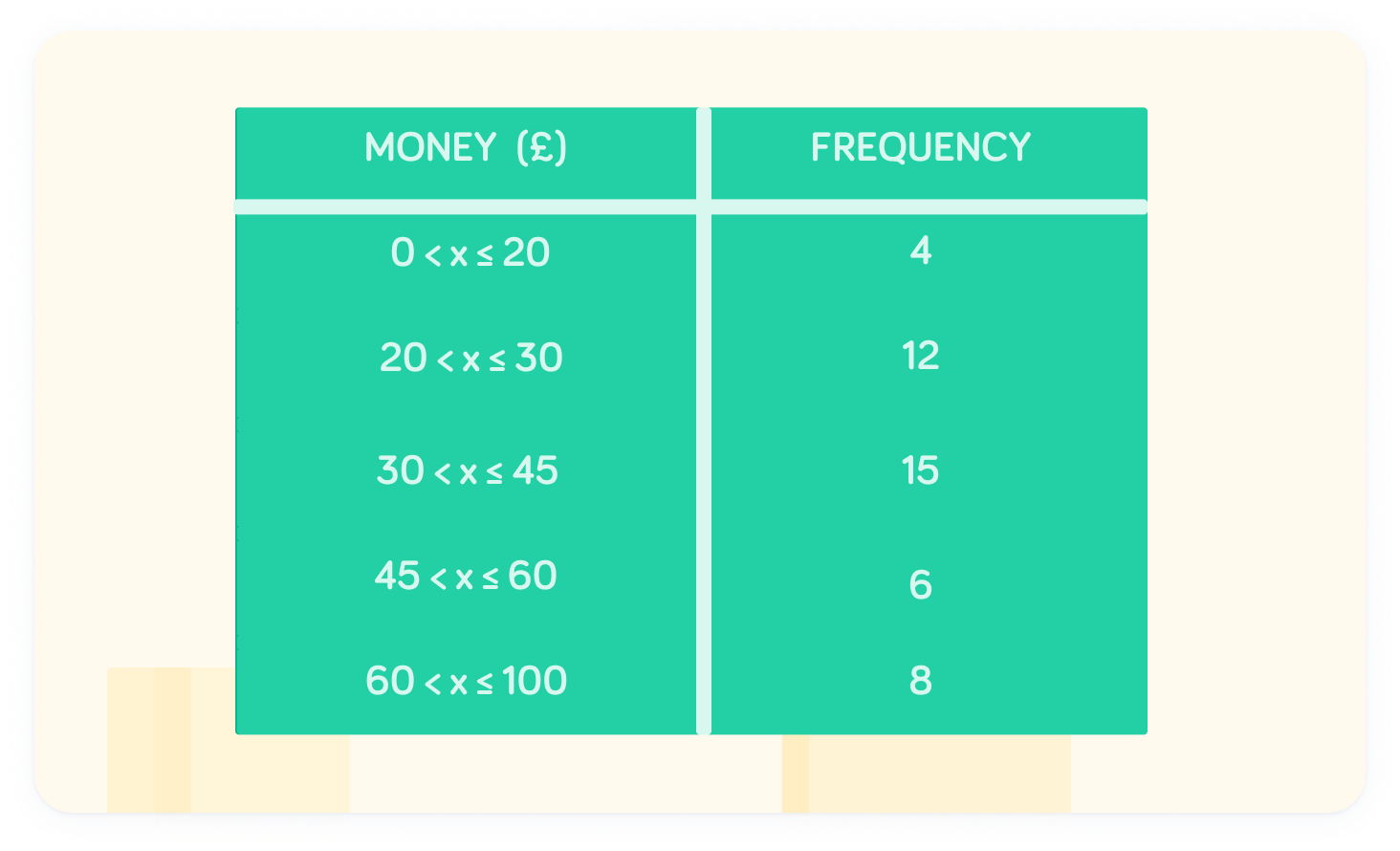
The class width is the size of the interval

Notice that the class width is different for each interval.

3

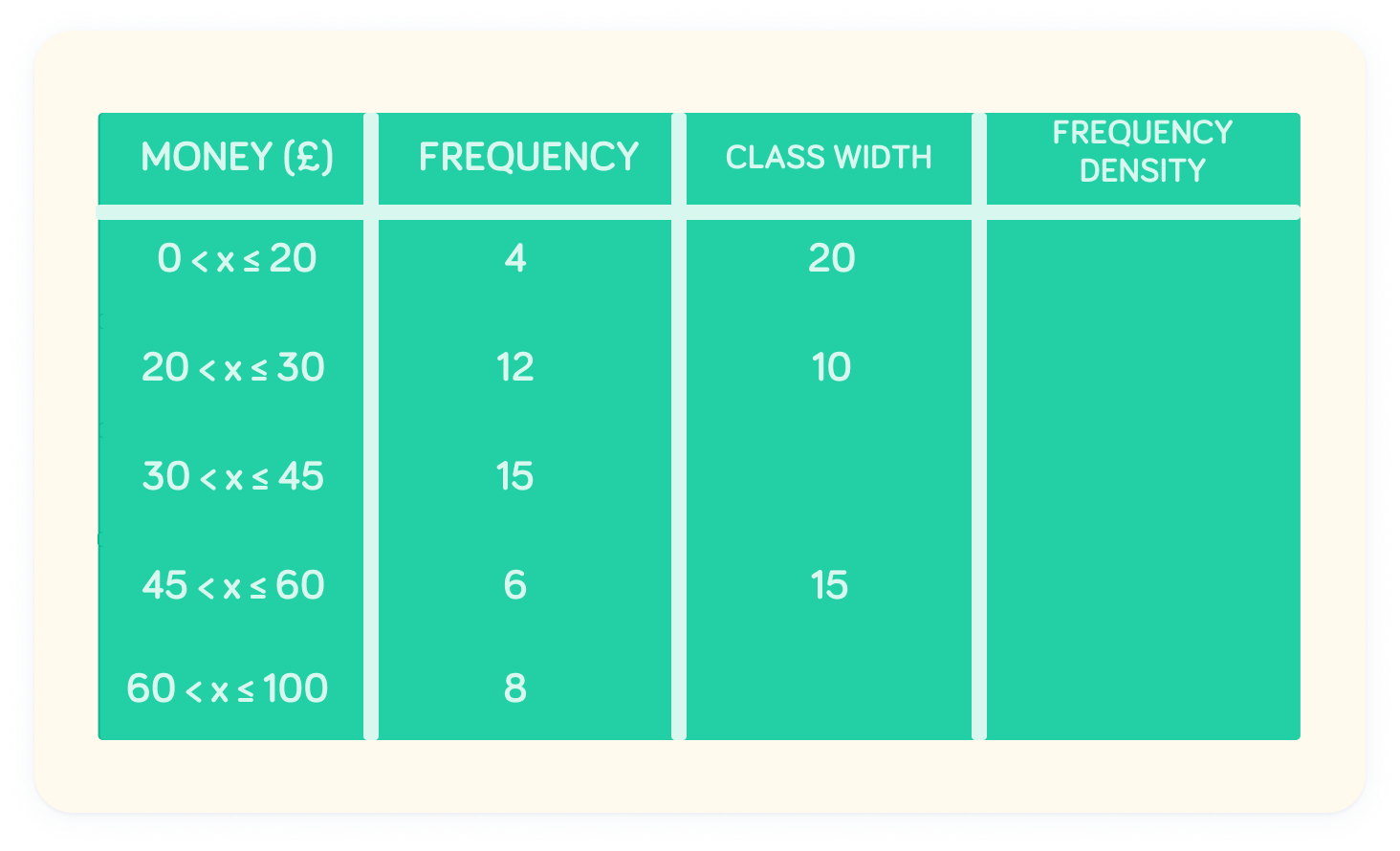
What is the class width of the interval $30<x\leq 45$ ?

4

What is the class width of the interval $60<x\leq 100$ ?

5

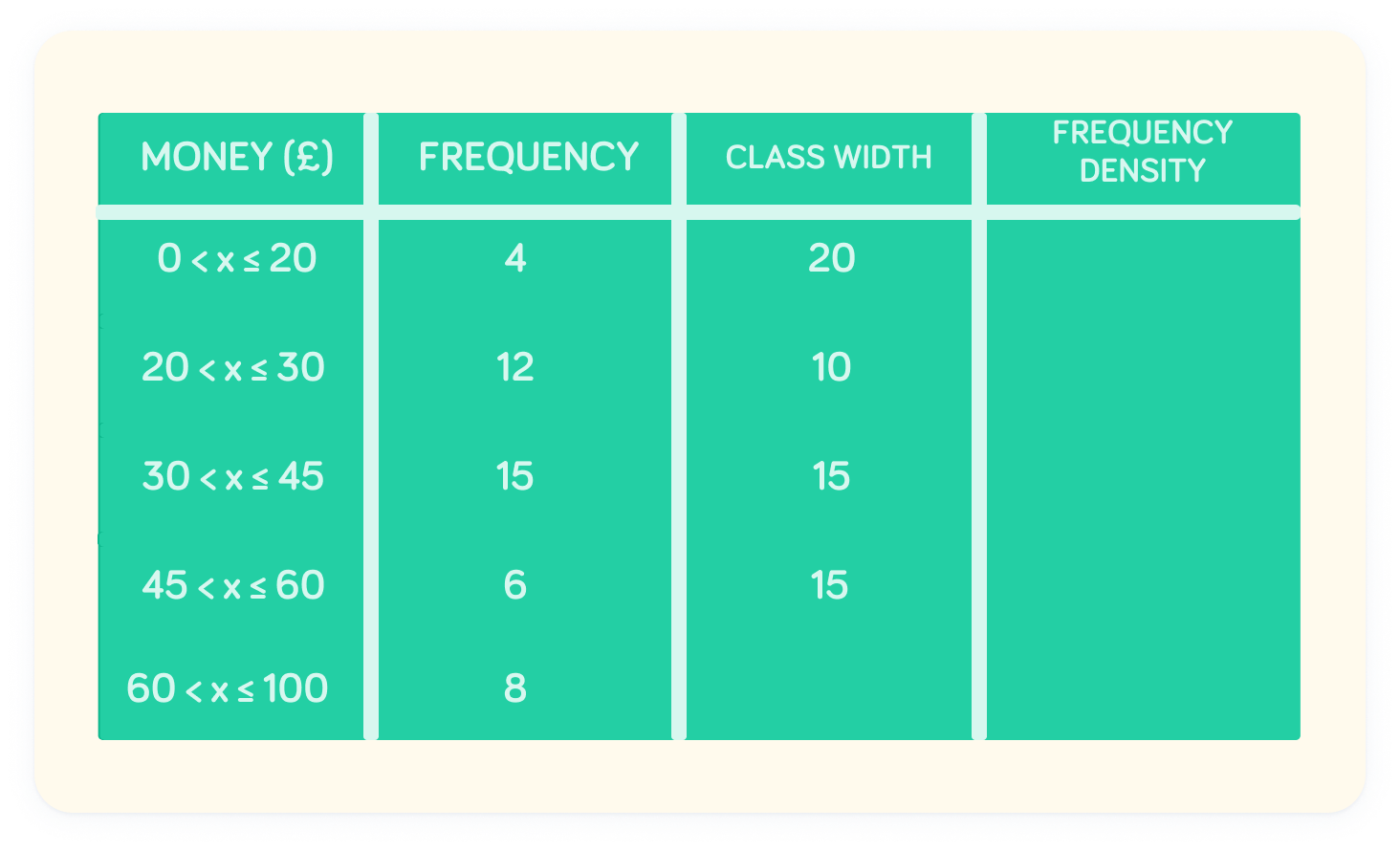
Now we can work out the frequency density

This is a measure of the area of the bar (like a bar chart). The formula for frequency density is given above.

6

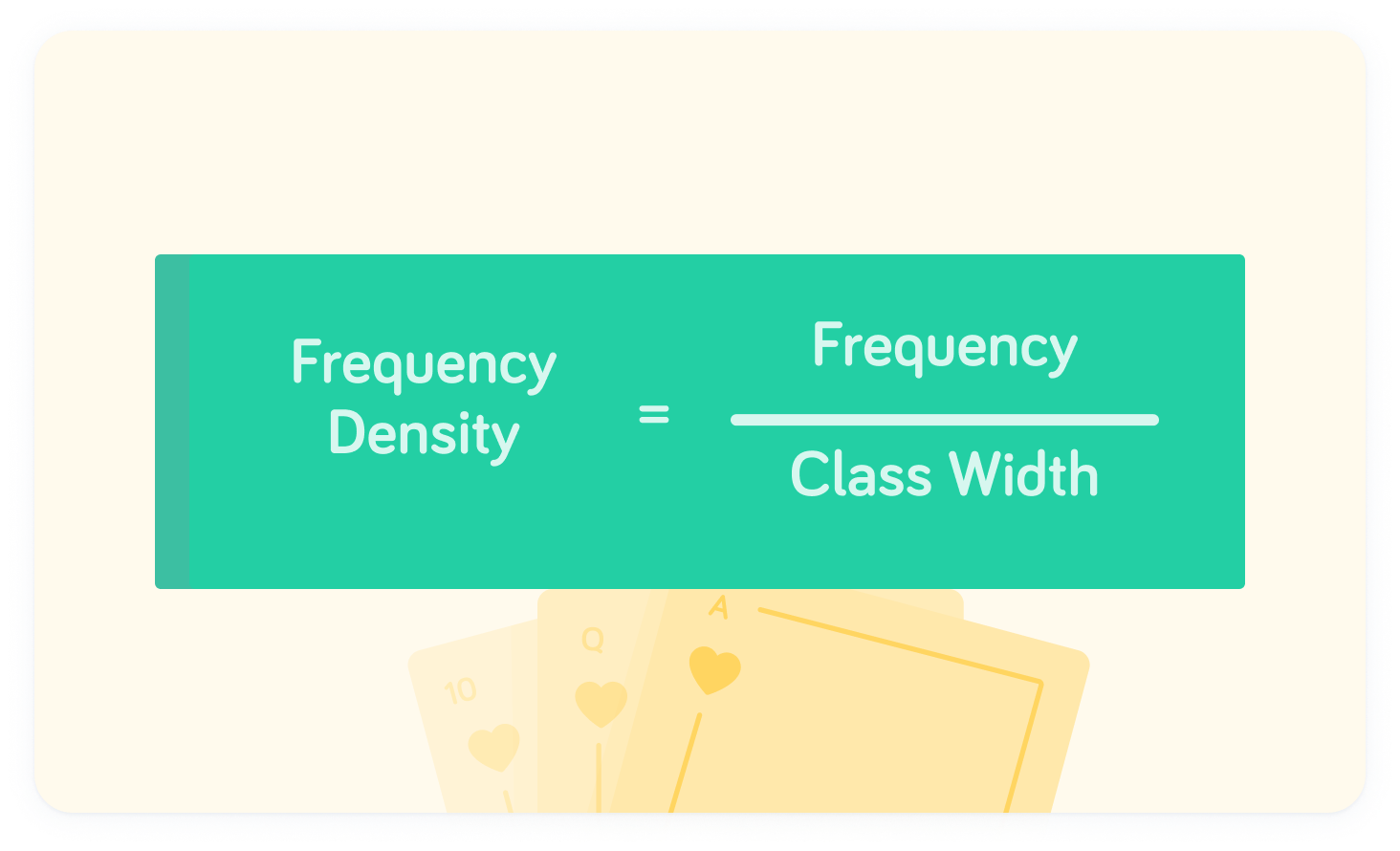
The frequency density measures the area

The frequency density for the interval $0<x\leq 20$ is $\dfrac{4}{20}=0.2$

7

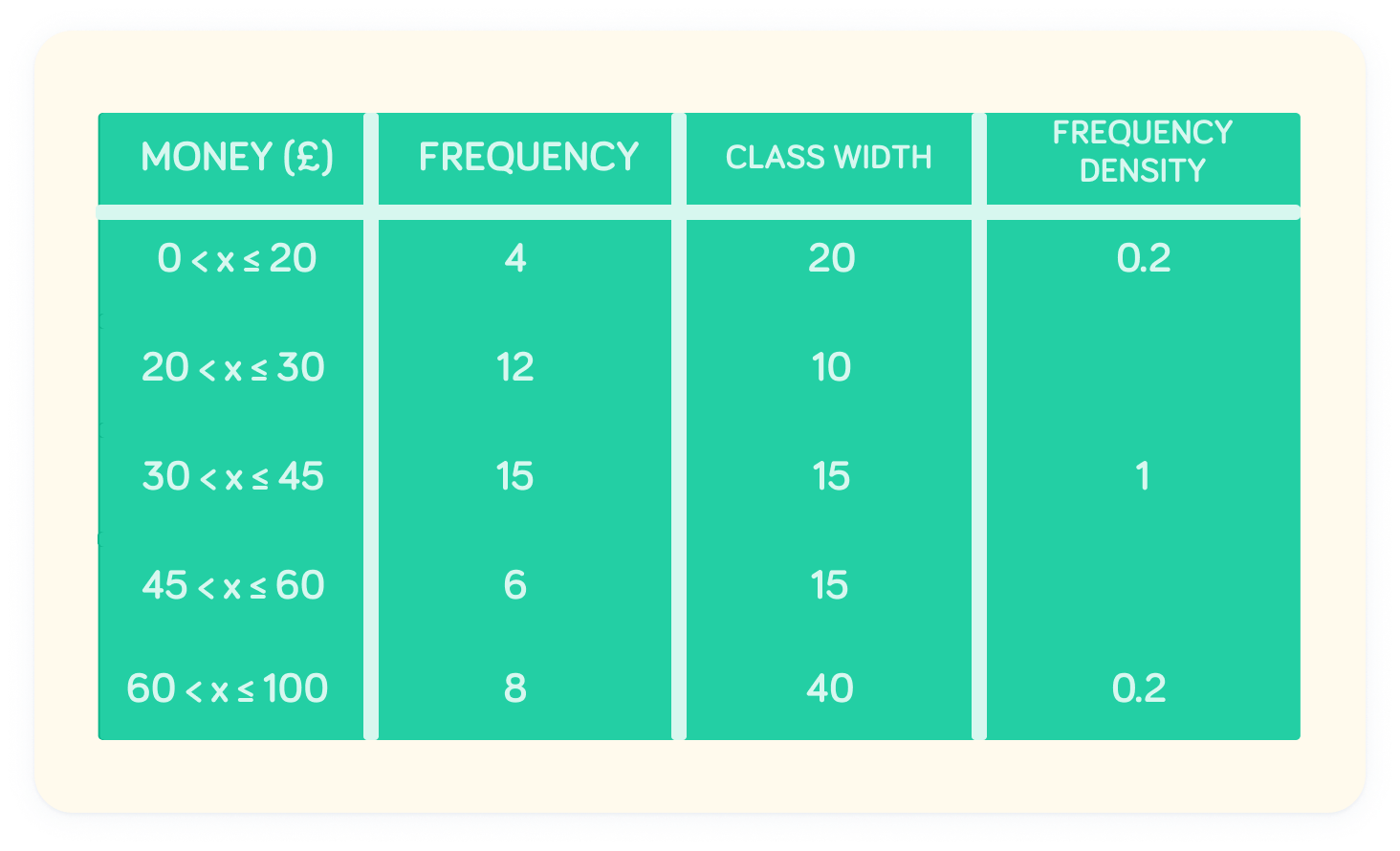
What is the frequency density at the interval $20<x\leq 30$ ?

8

At $20<x\leq 30$ , the frequency density is 1.2

$\dfrac{12}{10}=1.2$

9

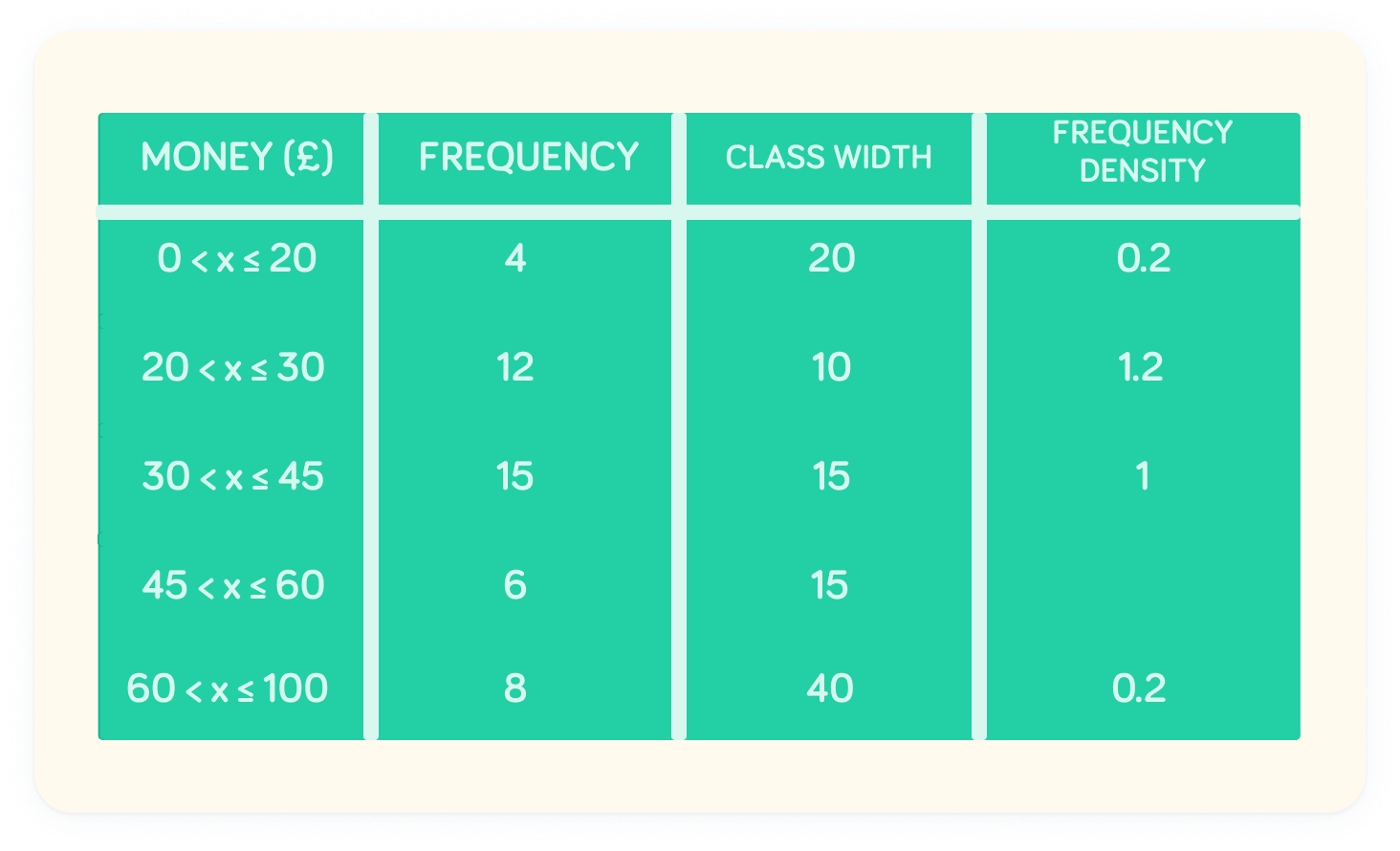
What is the frequency density at the interval $45<x\leq 60$ ?

10

At $45<x\leq 60$ , the frequency density is 0.4

$\dfrac{6}{15}=0.4$

11

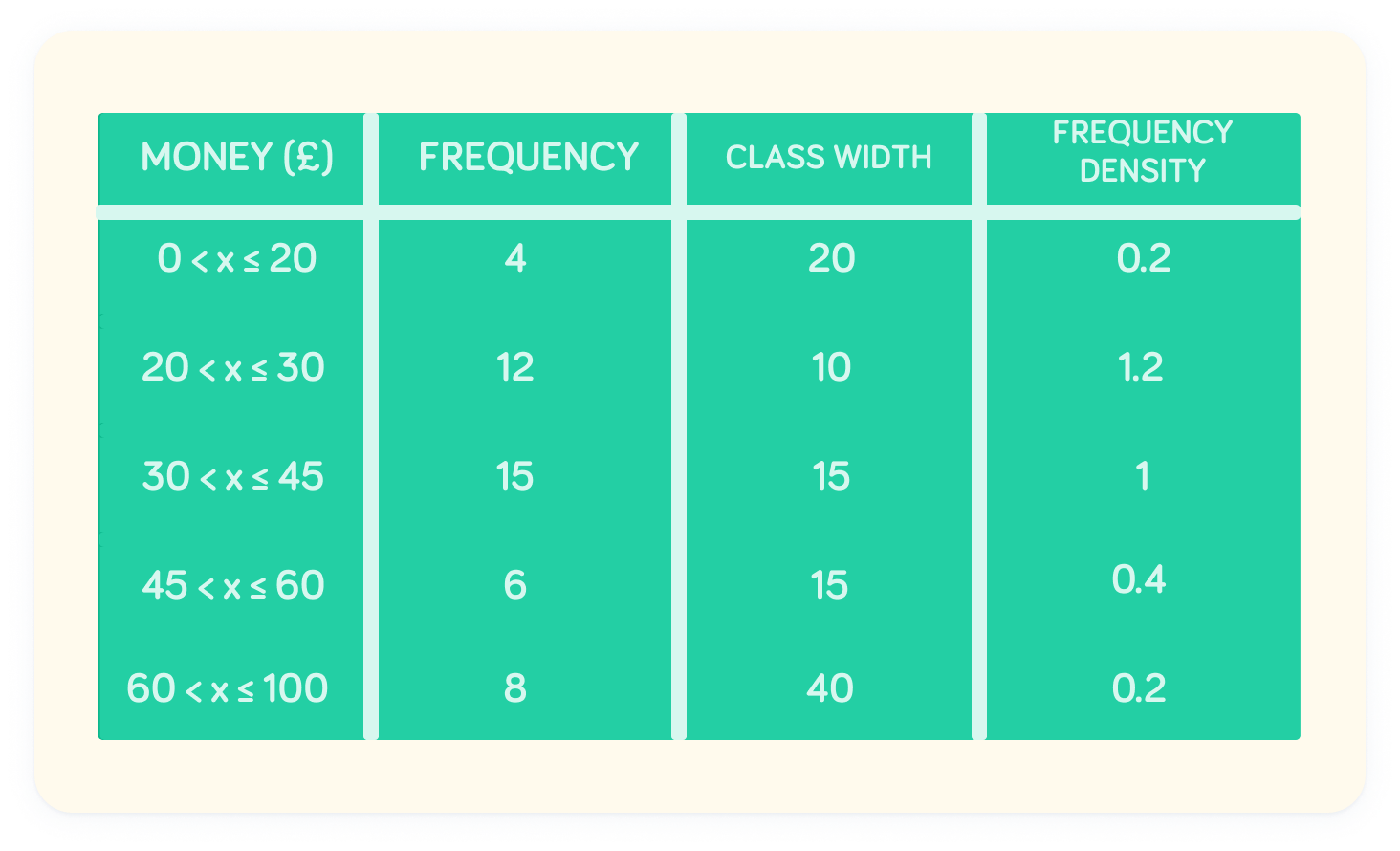
Nice!

Now we have the frequency density values, we can plot a histogram.