Probability & Statistics

YOU ARE LEARNING:

Histograms: Estimating the Median

Histograms: Estimating the Median

We can use a special method called linear interpolation to find the median from a histogram.

Histograms are plotted from grouped data, so we can't be sure of the individual data they represent. We use a special method to estimate the mean since we cannot observe it directly.

This method is called linear interpolation. It involves finding a proportional relationship between the position and value of the median within its grouped interval.

What is the correct formula to find the frequency after observing a histogram?

Here is a table with the intervals, frequency densities and frequencies

We can calculate the frequency with the formula $frequency \space density \times class \space width$ .

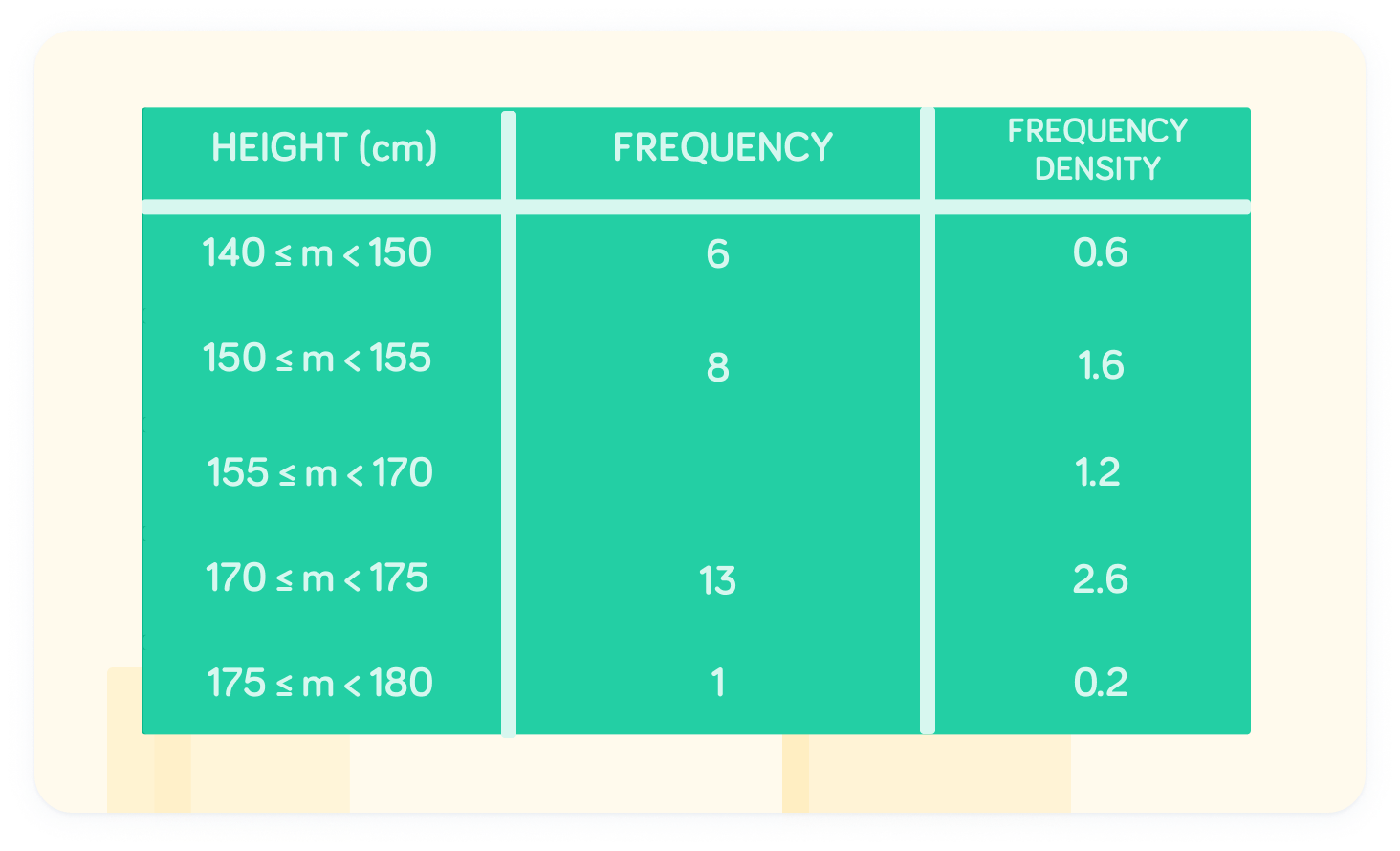
What is the frequency at the interval $155\leq m <175$ ?

The frequency is 18 at the interval $155\leq m <175$

$1.2 \times 15 = 18$

The cumulative frequency can identify the median

We need to identify which interval the median value is located in.

What is the missing cumulative frequency value?

The median is the 23rd value

Therefore, we can see that it is located in the interval $155 \leq m <170$ . The 23rd student, therefore, has a height between 155cm and 170cm.

We can represent this on a number line

The number line presents a schematic showing where the median lies relative to the upper and lower bounds of the interval.

Now we can identify a proportional relationship

The proportion of the position of the median is the same as the proportion of the value of the median (relative to the upper and lower bounds of the interval): $\dfrac{23-14}{32-14}=\dfrac{Q2-155}{170-155}$

We can simplify this equation

$\dfrac{23-14}{32-14}=\dfrac{Q2-155}{170-155} \space \rightarrow \space $$\frac{9}{18}=\frac{Q2-155}{15}$

By rearranging, we can find the median

$\dfrac{9}{18}=\dfrac{Q2-155}{15} \space \rightarrow \space 7.5=Q2-155$

If $7.5=Q2-155$ , what is $Q2$ ?

The median is $162.5cm$

Great work! Remember this is only an estimate, since we cannot observe the median directly in grouped intervals.