Probability & Statistics

YOU ARE LEARNING:

Mean from a Grouped Frequency Table

Mean from a Grouped Frequency Table

In grouped frequency tables, it is a little harder to find the mean as we only have groups of values. However, we can use group midpoints to find an estimation of the mean.

When data is grouped in a table, it is harder for us to calculate an accurate value for the mean as we do not have individual data. Therefore, we can only calculate an estimate.

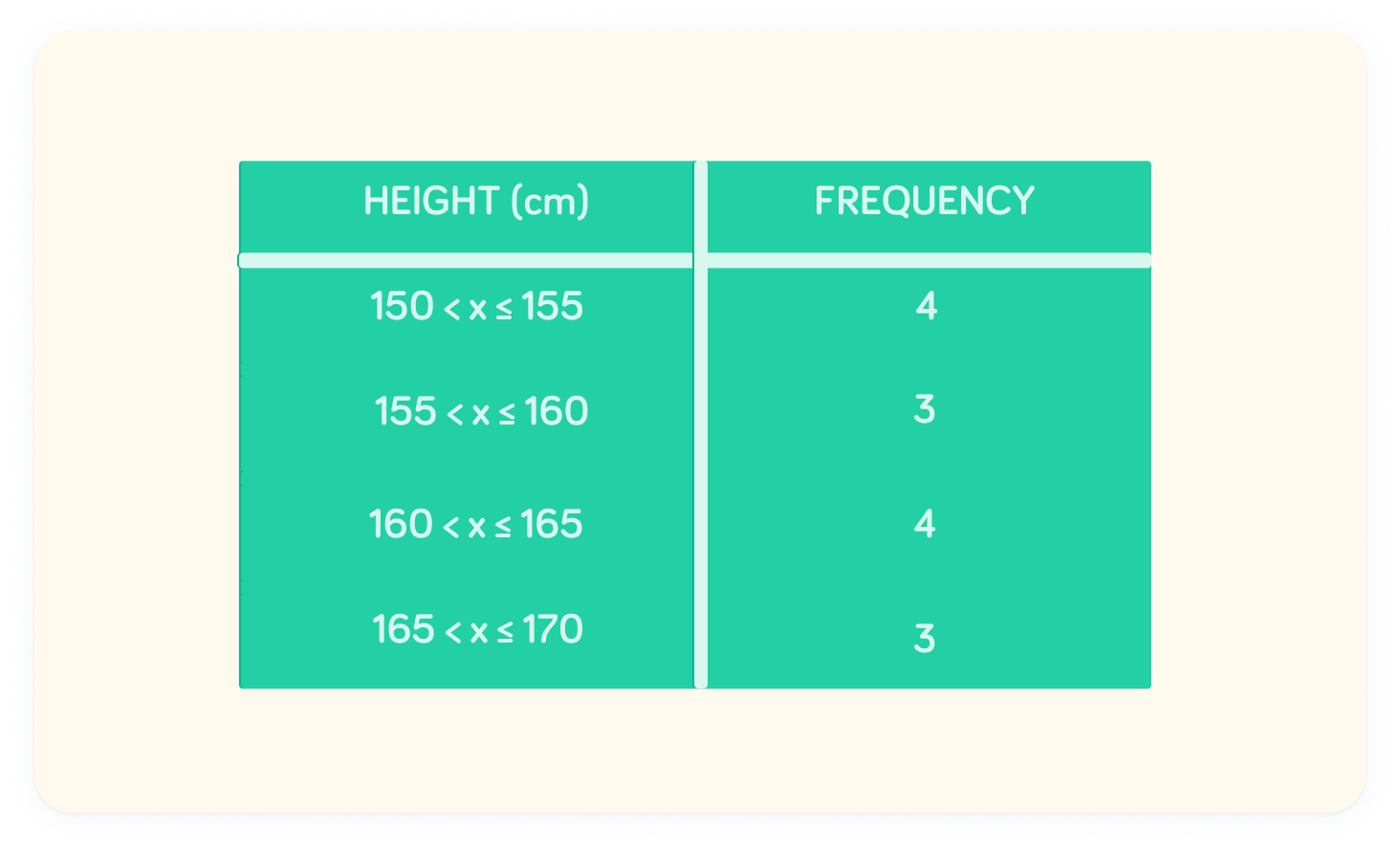
The table shows the heights of a small group of students

We know there are 4 people with a height in the interval $150 < h\leq 155$ , but we do not know exactly how tall each of these 4 people are.

This is the formula for the mean

Without information on the individual height of the students, we will not be able to calculate a “sum” of all the heights. Instead we must use an estimate. A good estimate here is the midpoint of each interval.

What is the midpoint of the group $150 < h \leq 155$ ?

The midpoint of $150 < h \leq 155$ is $152.5$

In finding the midpoint, we assume 4 people with the height of 152.5cm, 3 people with the height of 157.5cm, 4 people with the height of 162.5cm and 3 people with the height of 167.5cm.

Multiply the frequency and midpoints together

This will enable us to find an estimate for the sum of all heights.

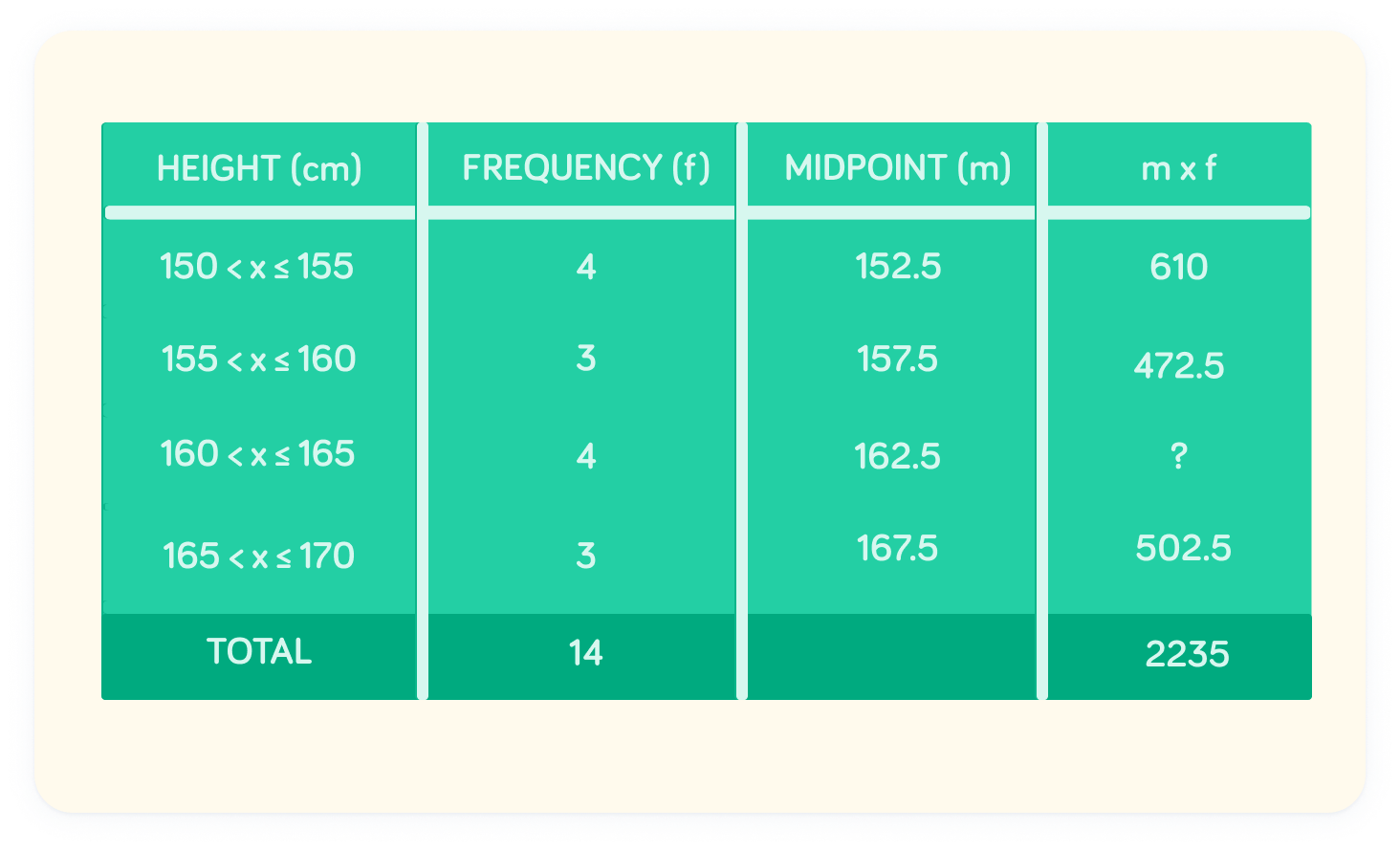
What is the value marked "?" in the table?

The missing value is $650$

We can sum each of these values up to a total of $2235$

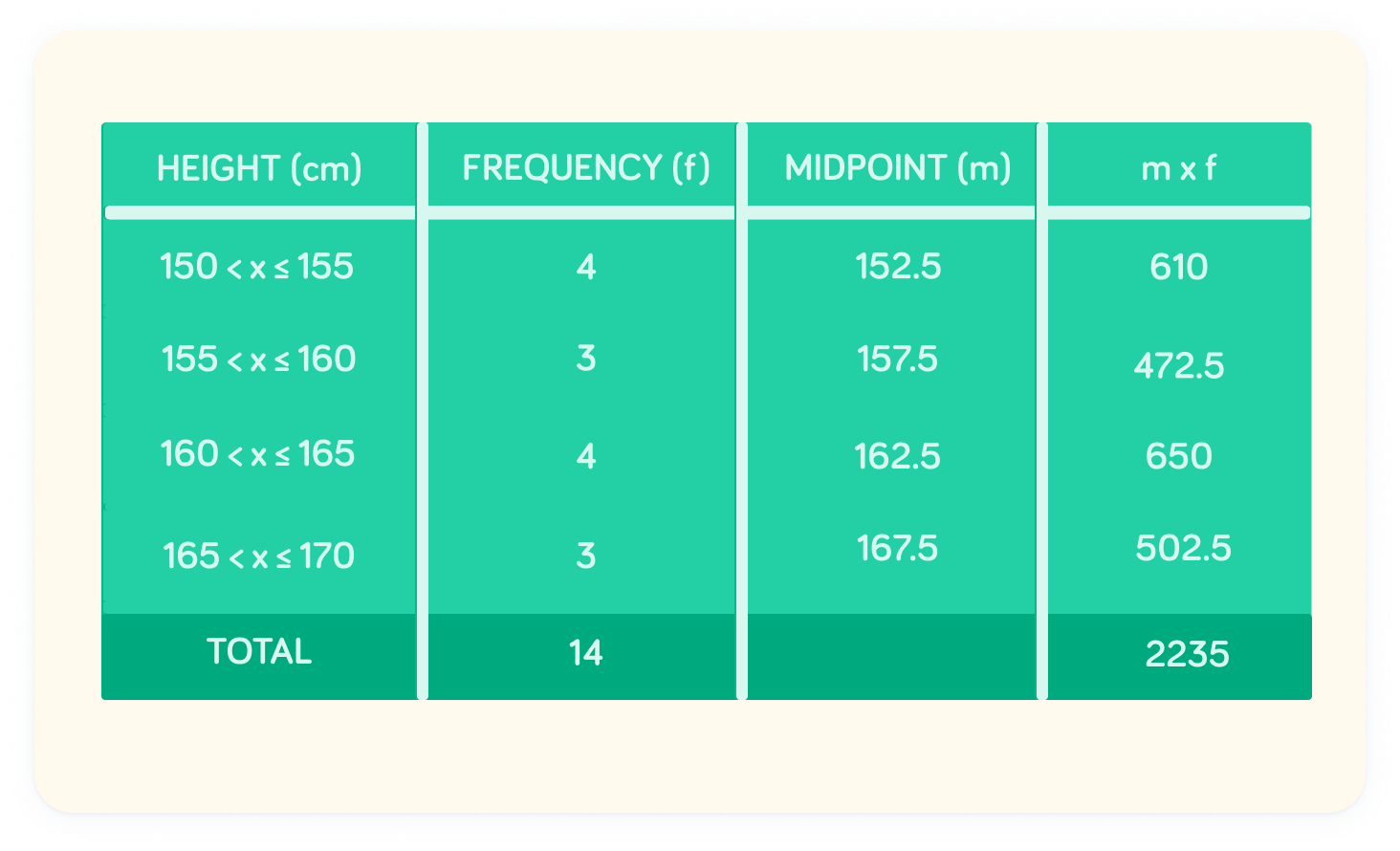
Now we can find the mean

The sum of all values is $2235$ , and the total number of values is $14$ .

What is the mean height? Give your answer to 1 decimal place

The mean height is $159.6cm$

We can find this by dividing $\dfrac{2235}{14}=159.6$ . Remember that this is only an estimate for the mean, since we do not have any individual values.