Basic Concepts in Physics

YOU ARE LEARNING:

The Formula for Acceleration

The Formula for Acceleration

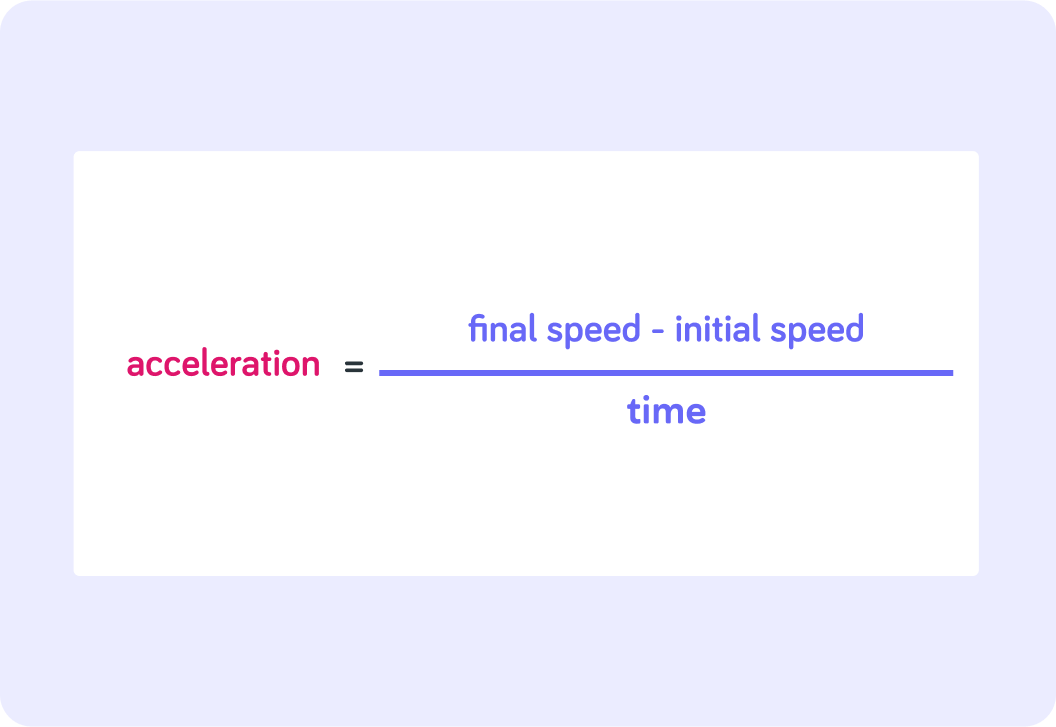
You find acceleration by dividing the change in velocity by time.

An example

How fast is this cyclist going?

10 seconds later, how fast is the cyclist going?

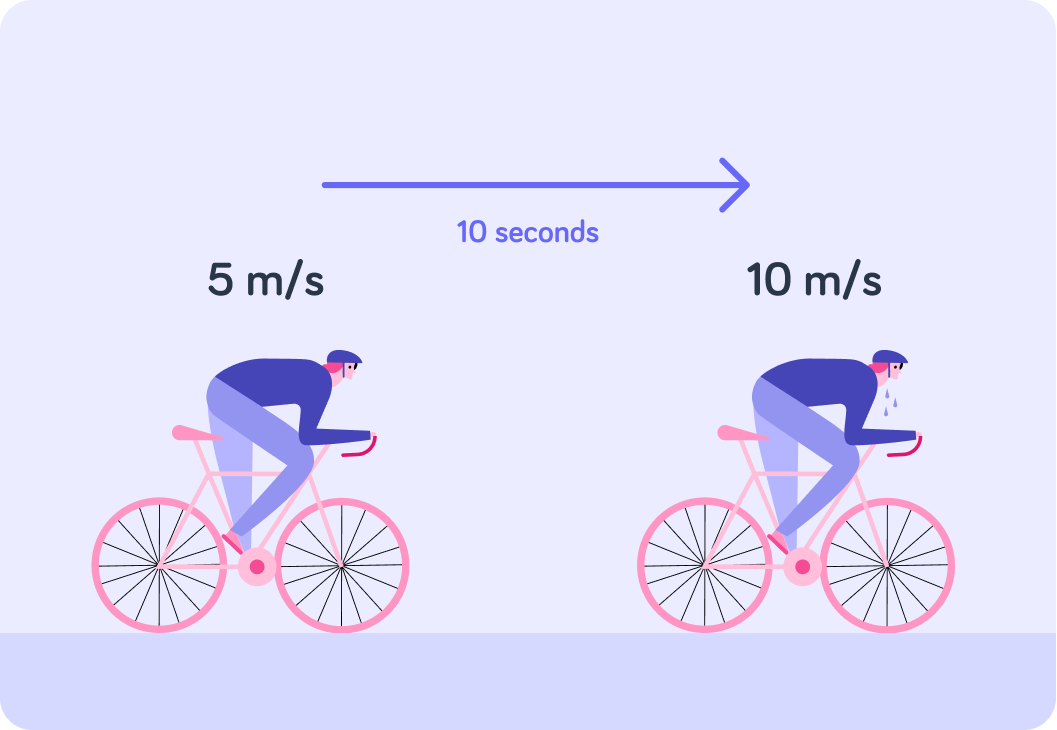
How much faster is $10 \space m/s$ than $5 \space m/s$ ?

So over the course of $10 \space s$ , this cyclist got $5 \space m/s$ faster. How many $m/s$ did the cyclist get faster every second?

So every second, this cyclist accelerated by $0.5 \space m/s$

You say that his acceleration was $0.5 \space m/s^2$

The unit $m/s^2$ will be explained a little later in this lesson.

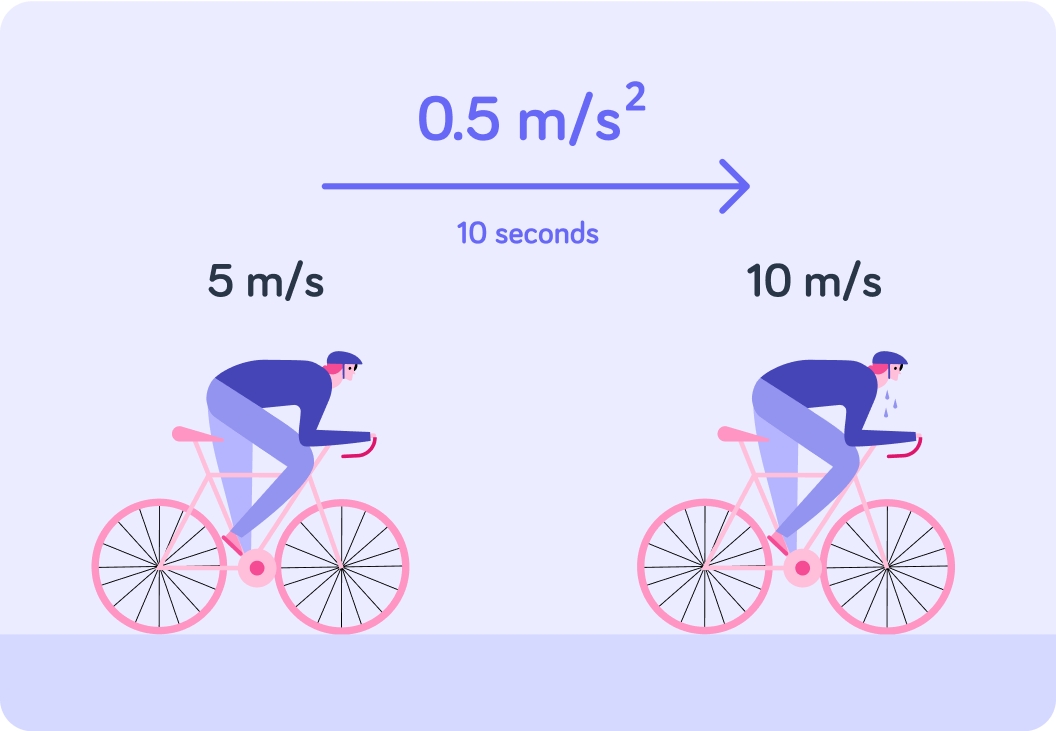
You worked out the cyclist's acceleration like this $\frac{10 \space m/s - 5 \space m/s}{10 \space s}=0.5 \space m/s^2$ . So what is the correct formula for acceleration?

The unit $m/s^2$ explained

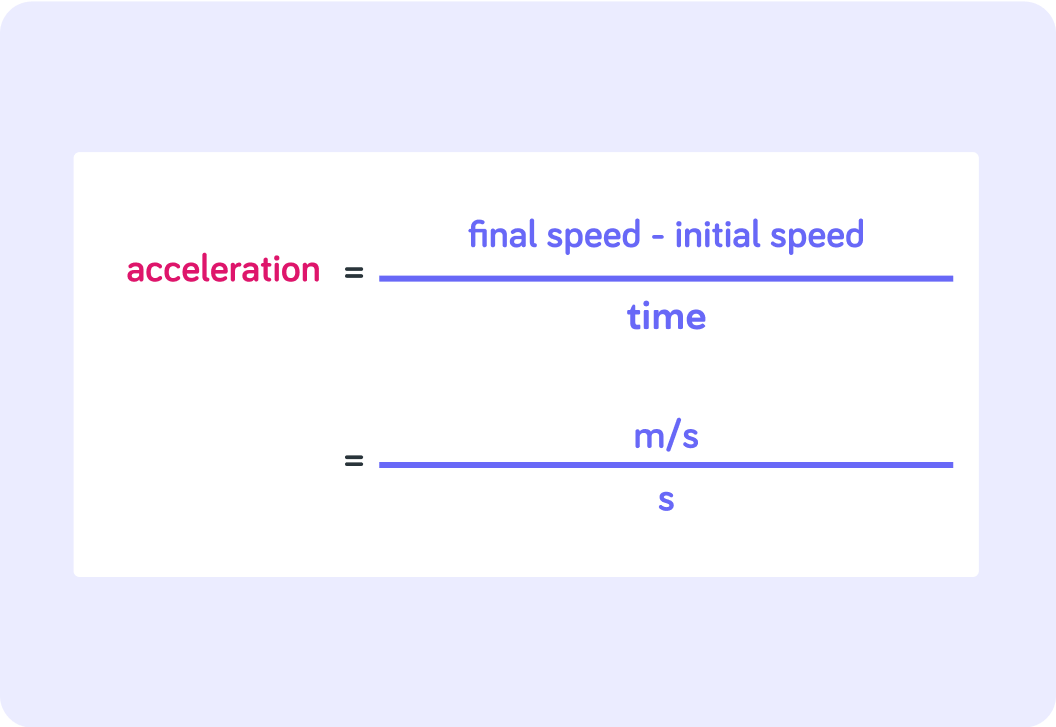
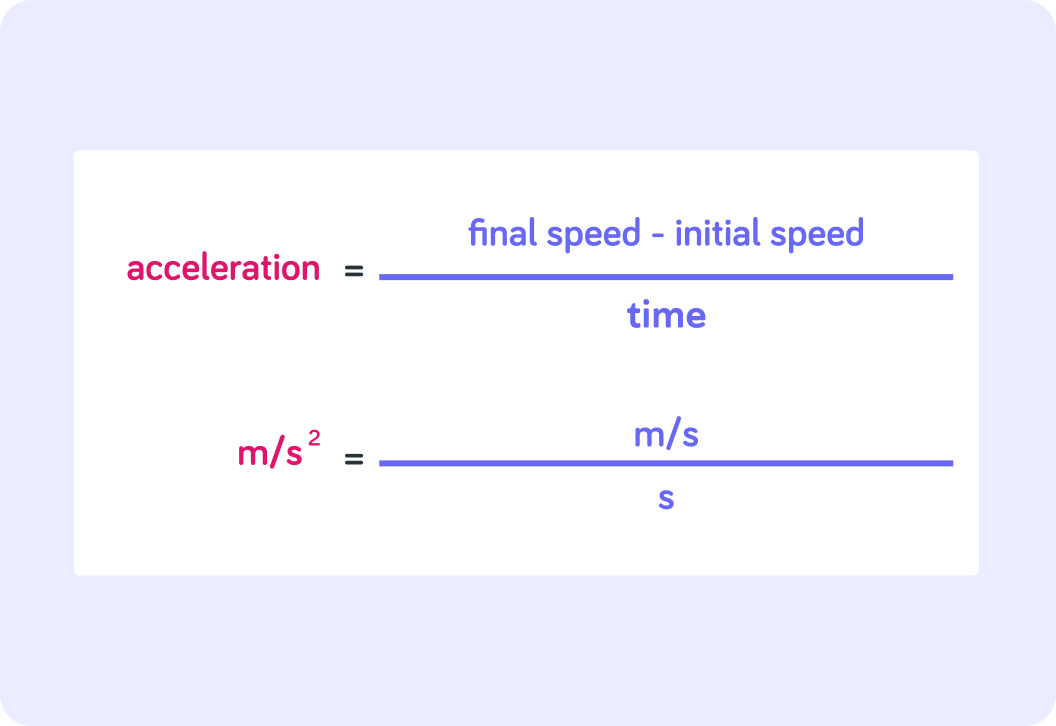
This is the formula for acceleration. What is the unit you have used for speed in this lesson?

What is the unit you have used for time in this lesson?

The image now also shows the formula in units

It shows that acceleration is a change in meters per second per second, because $m/s$ is divided by $s$

$\frac{m/s}{s}$ is the same as $\frac{m}{s \times s}$ . How can you also write $s \times s$ , using powers?

$\frac{m/s}{s}$ is the same as $\frac{m}{s \times s}$ which is the same as $\frac{m}{s^2}$

That is why the unit for acceleration is $m/s^2$ and not simply $m/s$ (which is the unit for speed!).

Acceleration is a change in metres per second per second.

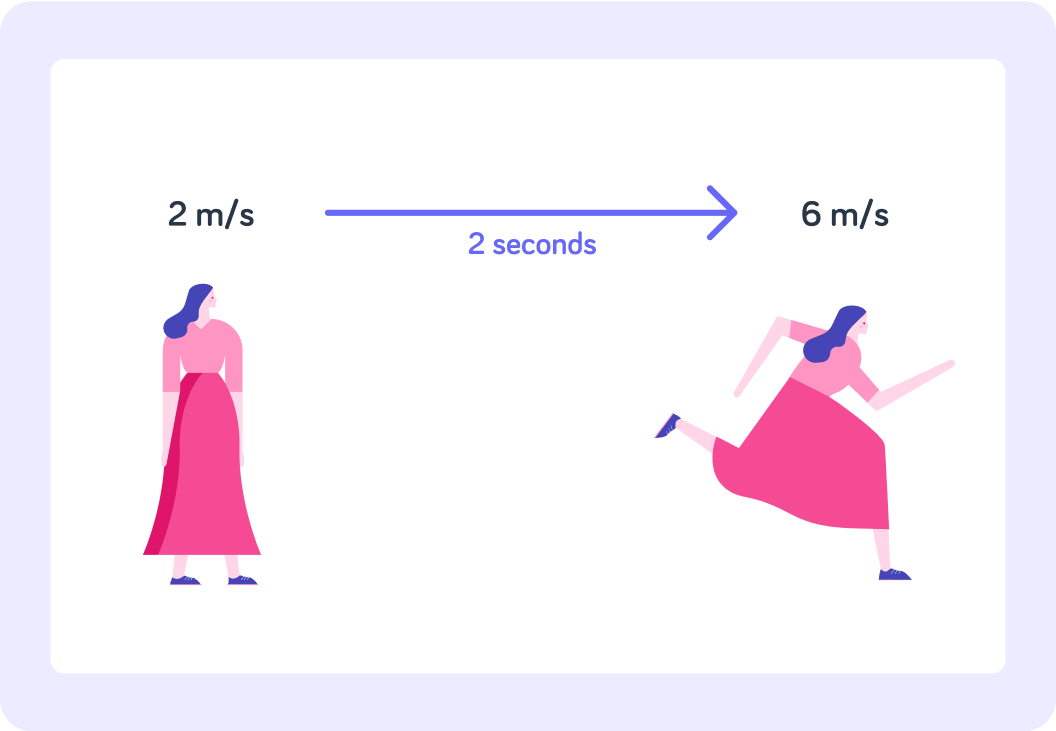
What is this woman's acceleration in $m/s^2$ ?

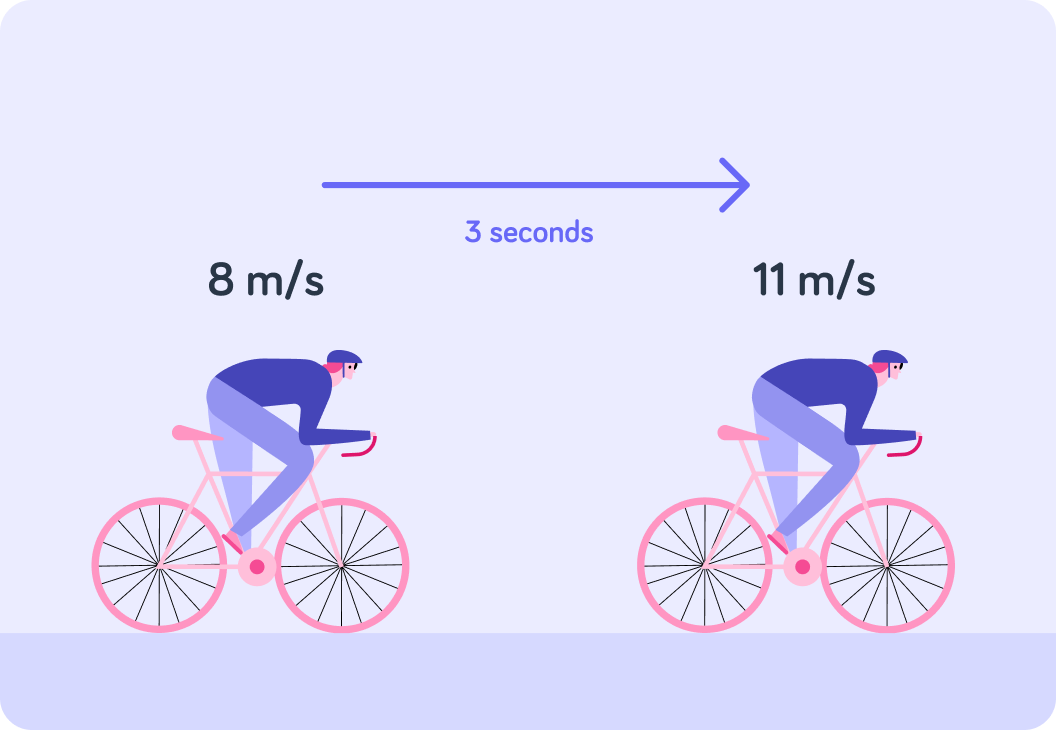
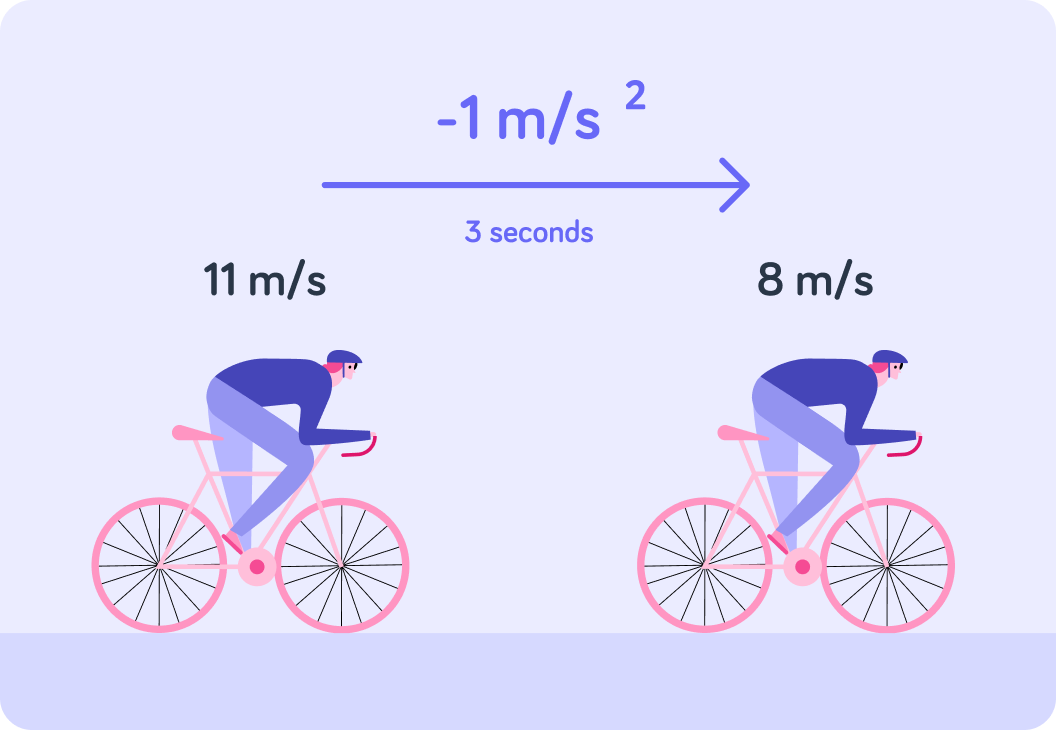
What is this cyclist's acceleration in $m/s^2$ ?

Careful now!

What is this cyclist's initial speed?

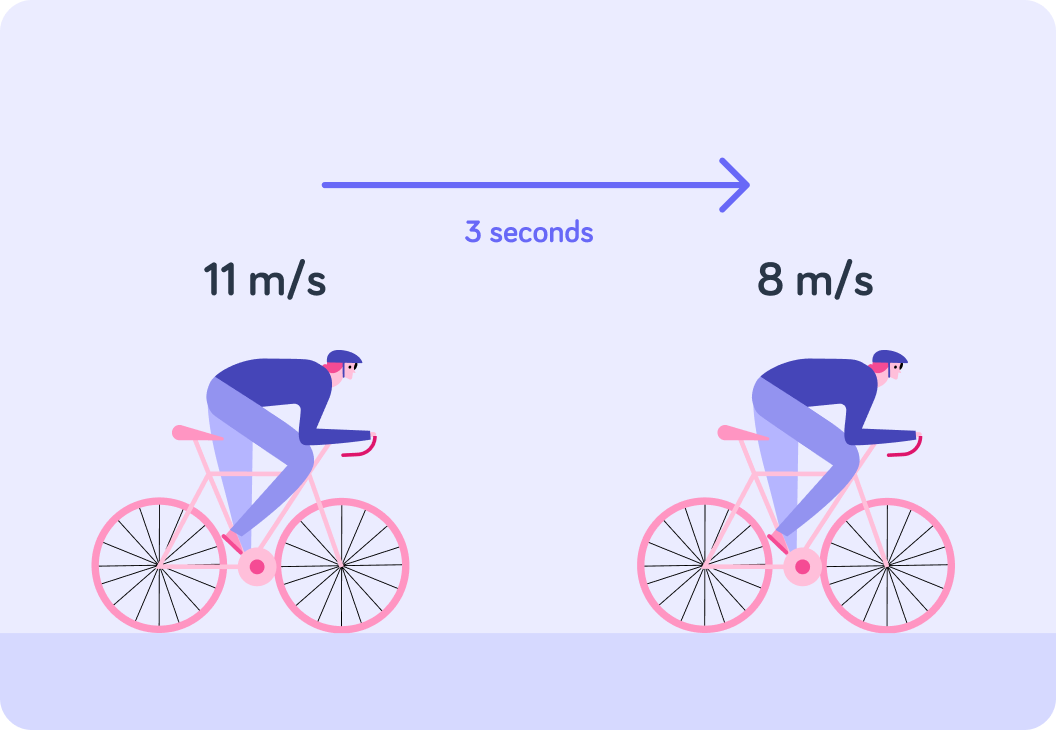
What is his final speed?

Is this cyclist speeding up or slowing down?

Use the formula $acceleration = \frac{final \space speed - initial \space speed}{time}$ as normal. What is the cyclist's acceleration?

So acceleration can be negative!

If an object is slowing down, it's still "accelerating", but the acceleration is negative.

Summary!

You calculate acceleration like this

$acceleration = \frac{final \space speed - initial \space speed}{time}$

This gives you the unit $m/s^2$

You essentially say $\frac{m/s}{s}$ which is the same as $\frac{m}{s \times s}$ or $\frac{m}{s^2}$

Acceleration is a change in metres per second per second.

If an object is slowing down it is still "acceleration"

It just means that acceleration will be negative because $final \space speed - initial \space speed$ will give a negative value.