Basic Concepts in Physics

YOU ARE LEARNING:

What Is Acceleration?

What Is Acceleration?

Acceleration is a change in velocity.

An example of acceleration

This woman is moving at $3 \space m/s$ , so this image tells us the woman's _____________.

One second later the woman is moving at $7 m/s$ . What happened?

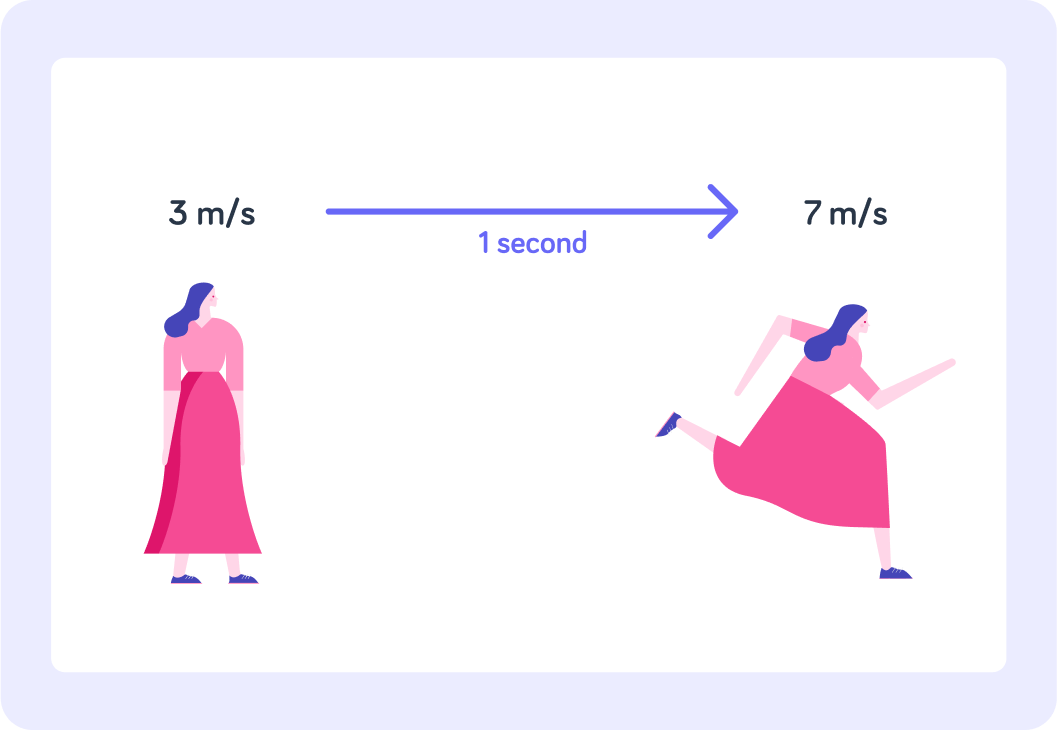
In other words, the woman has "accelerated"

Over the course of 1 second, she sped up from $3 \space m/s$ to $7 \space m/s$

Which one of these do you think has the fastest acceleration?

Speed and velocity describe how quickly an object travels. What best describes acceleration?

How to recognise acceleration

What type of graph is this?

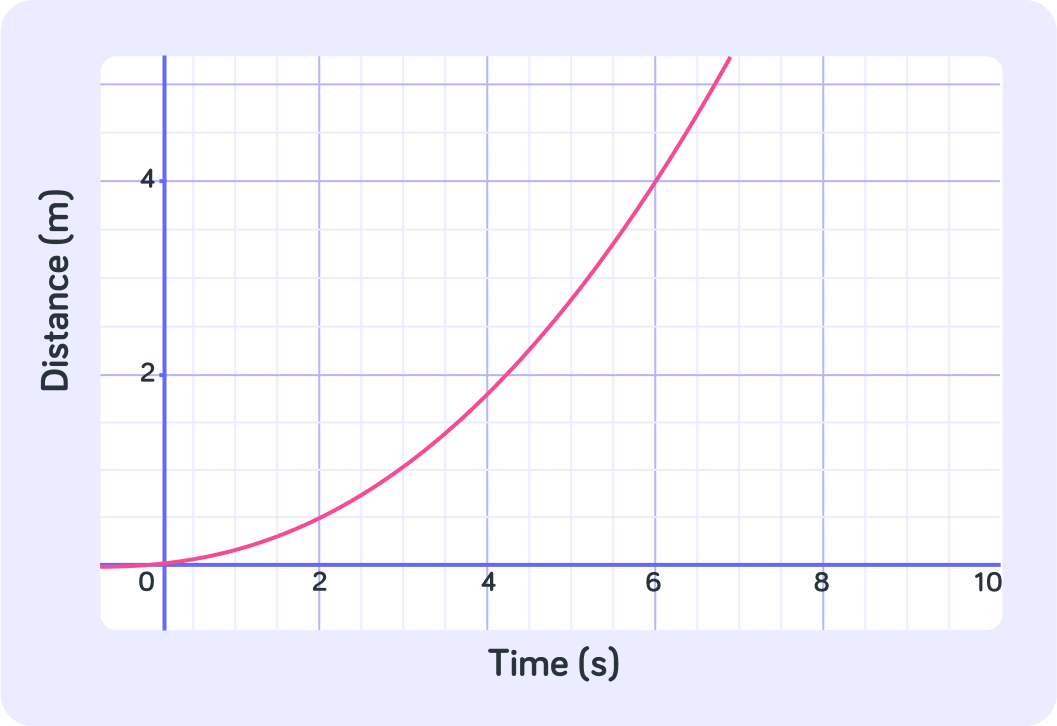
This is a distance - time graph.

It tells you the position of an object at any point in time.

What does the gradient of this D-T graph tell us?

So the gradient or slope of a D-T graph shows us the velocity the object has. Is this particular object travelling at a constant velocity?

So if the speed of this object is not constant, in 1 word what is it doing?

So, acceleration is the change in speed or velocity of an object.

This means that a D-T graph with a changing gradient, or a curved line, represents an accelerating object.

Acceleration and deceleration

What is this cyclist doing?

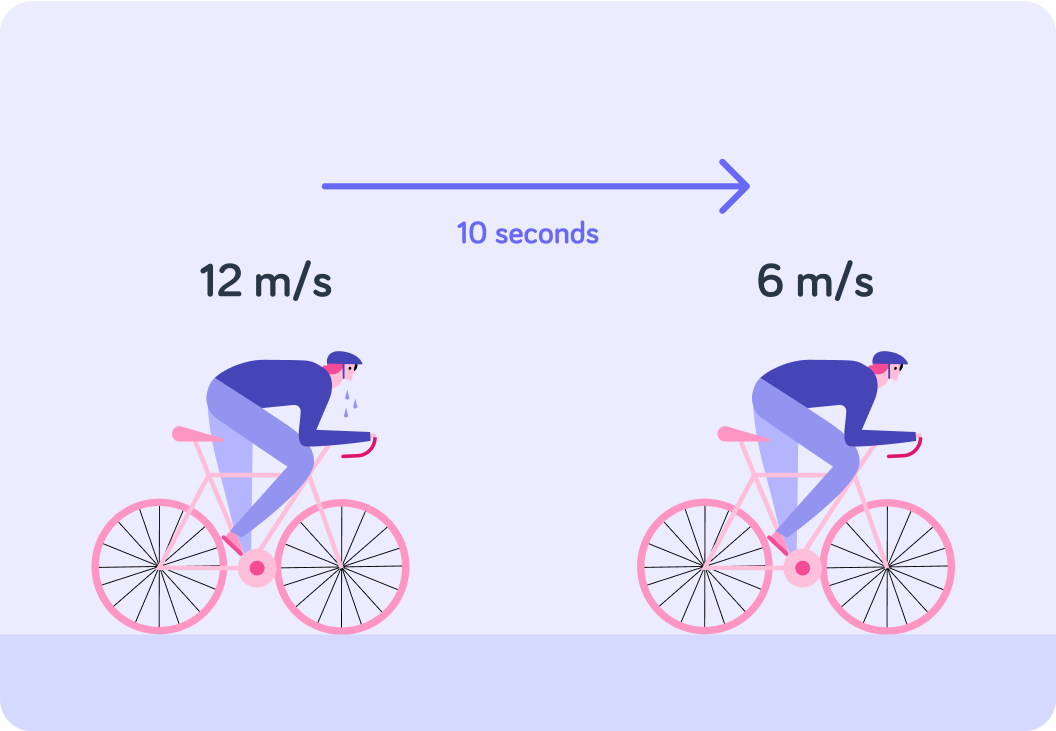
Is this cyclist accelerating?

The cyclist's acceleration is...

So this cyclist has a negative acceleration.

This is the same as saying that this cyclist is decelerating.

True or false: Accelerating at $-3 \space m/s^2$ is the same as decelerating at $3 \space m/s^2$

So acceleration can be either positive (speeding up) or negative (slowing down). Do you think you can also talk about both positive and negative deceleration?

So an object getting slower and slower has a negative acceleration whereas an object getting faster and faster has a positive acceleration. What does that make acceleration?

So, what is the best description of acceleration?

Summary!

Acceleration is how fast the velocity of an object changes

Or its rate of change of velocity.

Acceleration can be shown by a curved line on a D-T graph

This image is a good example of an object that is accelerating

Acceleration can be both positive and negative

Positive values for acceleration means speeding up, for example $5 \space m/s^2$

Negative values for acceleration means slowing down, for example $-5 \space m/s^2$

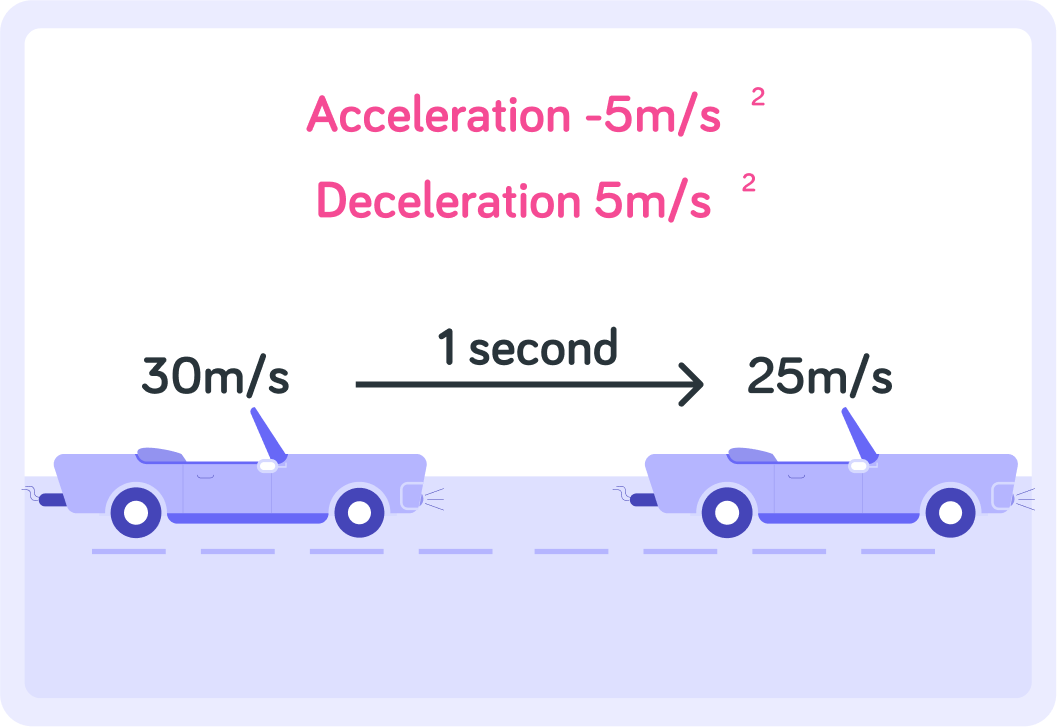
You can also use the word "deceleration" for negative acceleration

For example, accelerating at $-5 \space m/s^2$ is the same as decelerating at $5 \space m/s^2$

You cannot have negative values for deceleration

Deceleration always means slowing down, so it doesn't make sense to have both negative and positive values for deceleration.