Basic Concepts in Physics

YOU ARE LEARNING:

Uniform Acceleration

Uniform Acceleration

Distance and acceleration can be related to each other in a single equation.

What do you think uniform means?

So if an object has uniform acceleration, what does that mean?

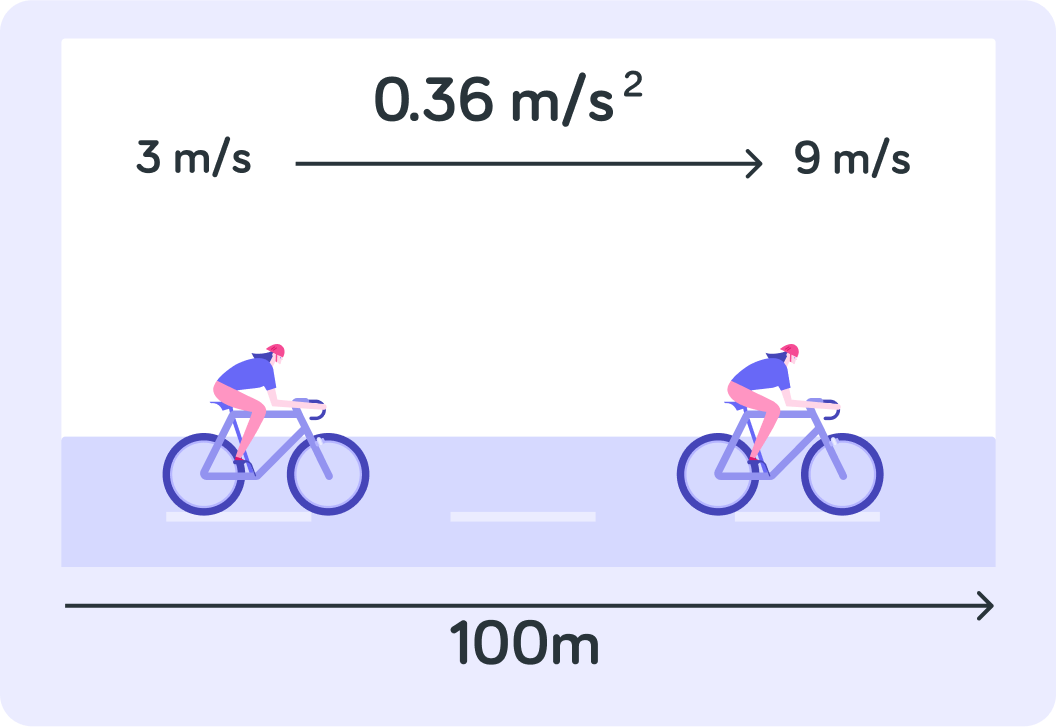
What is this cyclist's acceleration?

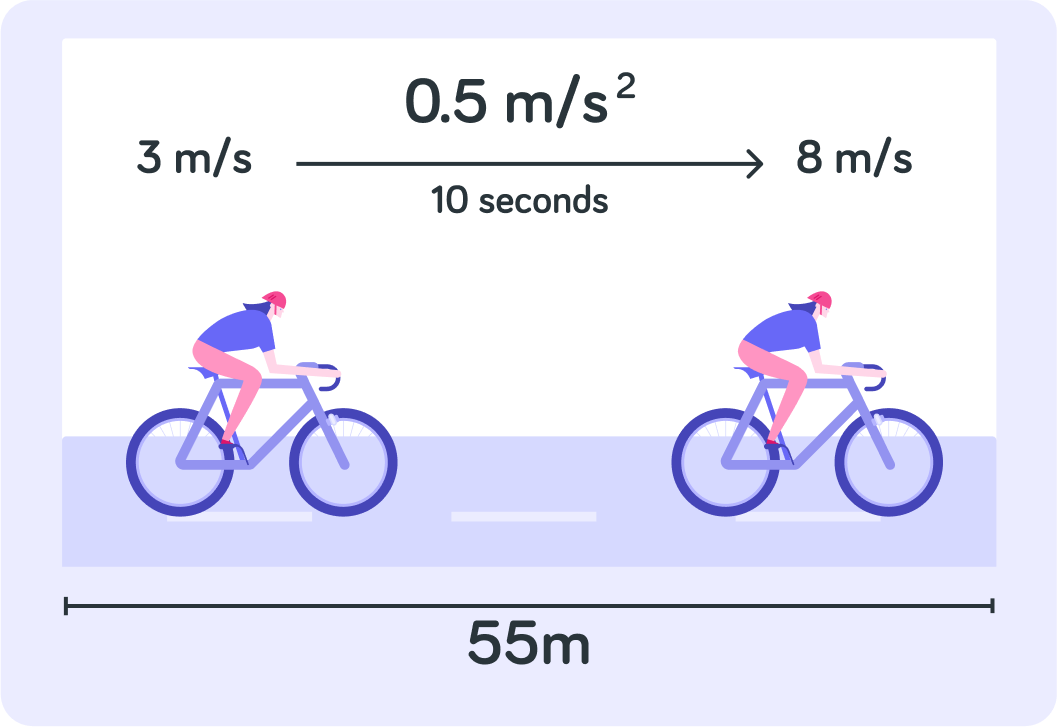
That means that the cyclist's velocity increases by $0.5 \space m/s$ every...

"Uniform acceleration" is the same as "constant acceleration"

For example, this cyclist's speed will accelerate by $0.5 \space m/s$ every second.

For uniform acceleration, we can use the following equation that links velocity, distance and acceleration.

$v^2-u^2=2as$

This lesson will teach you how and when to use this.

$v^2-u^2=2as$

First of all, with any equation, we have to define the variables. Starting with the most obvious one, what does $a$ stand for?

The equation for acceleration that we've already looked at is $a=\frac{\Delta v}{t}$ . This can also be written like this $a=\frac{v-u}{t}$ . What do you think $v$ and $u$ stand for, respectively?

So far we've defined $a$ as uniform acceleration, $u$ as initial velocity and $v$ as final velocity. What does that make $s$ ?

So we have $a$ for uniform acceleration, $u$ for initial velocity, $v$ for final velocity and $s$ for distance.

Let's now look at how to use this equation.

Calculating acceleration, $a$

With any question, the first thing you have to do is write down all the variables the question gives you. In this case, what variables do you know?

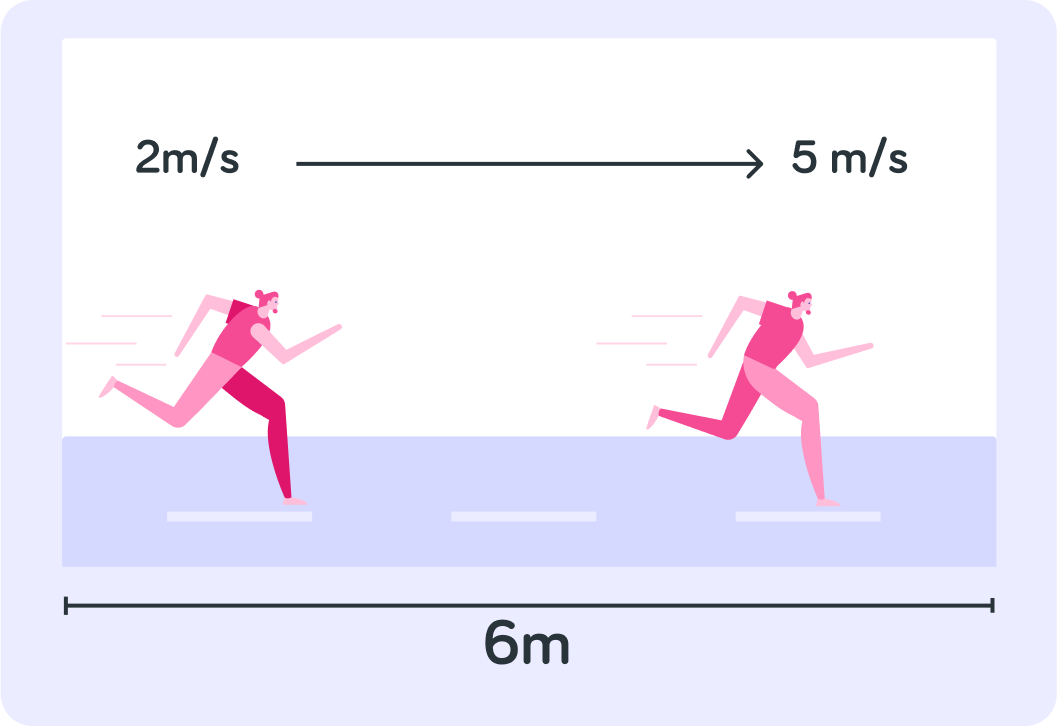
Ok, so now we have all of our variables defined.

$u=2\:m/s$

$v=5\:m/s$

$s=6\:m$

$a=\:?$

Now we need to rearrange our equation $v^2-u^2=2as$ to make $a$ the subject. What will this look like?

Great, now that we have all the information we need, calculate the acceleration using $a=\frac{v^2-u^2}{2s}$ .

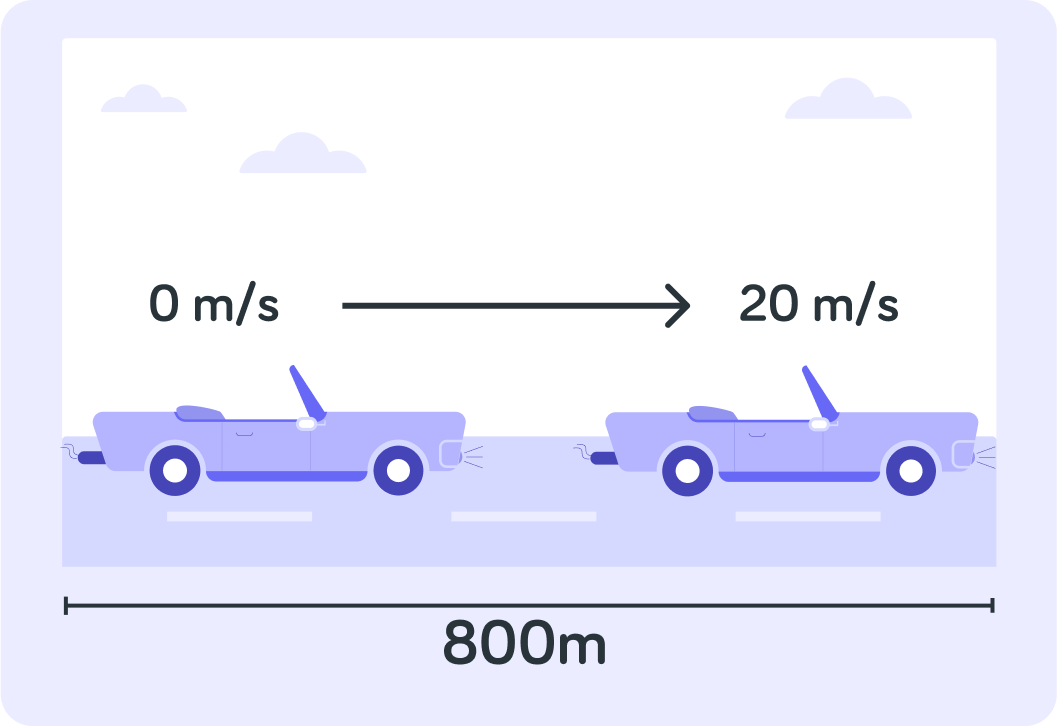
Use $a=\frac{v^2-u^2}{2s}$ to work out this car's acceleration. Give your answer to 2 decimal places.

A runner starts a race and uniformly accelerates at $0.5\:m/s^2$ until she reaches a velocity of $3\:m/s$ .

What information is missing from the above statement?

We know that we are going to be asked to find the distance the runner ran. Write $v^2-u^2=2as$ where $s$ is the subject.

Calculate how far the runner travelled until she reached her final velocity.

Calculating the final velocity, $v$

What values are given in this picture?

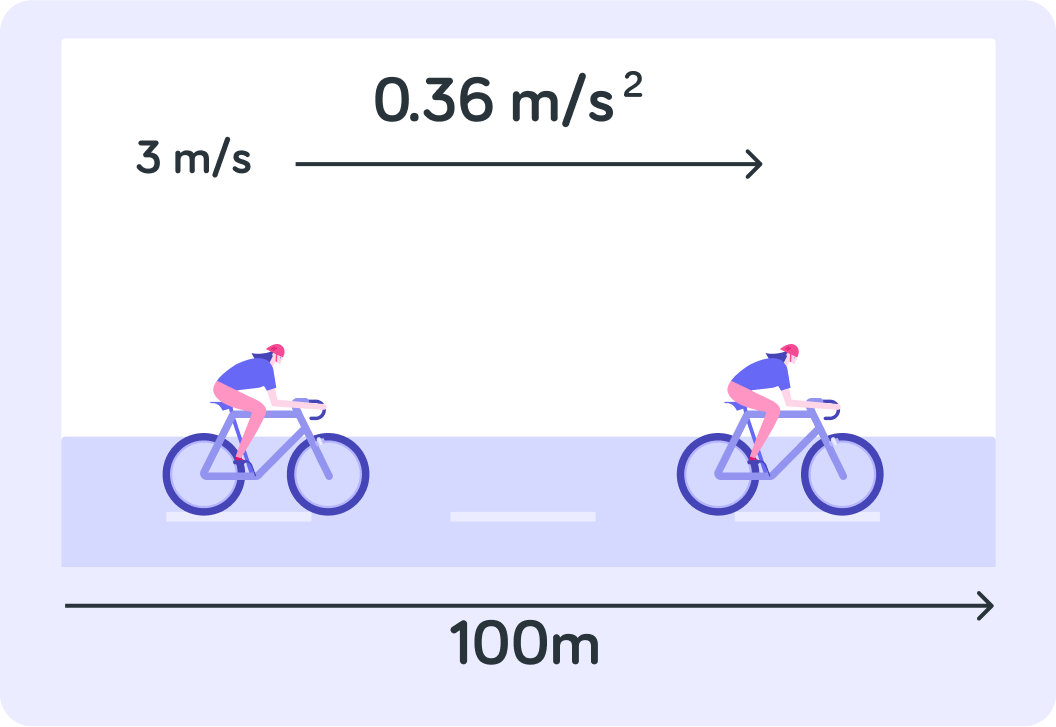
You can select multiple answers

So we are missing $v$ . How do we rearrange $v^2-u^2=2as$ to make the final velocity the subject?

Now use $v^2=u^2+2as$ to work out $v^2$ for this cyclist.

So $v^2=81 \space m/s$ . How do you work out the cyclist's final velocity, $v$ then?

So you worked out this cyclists final velocity using ...

$v=\sqrt{u^2+2as}$

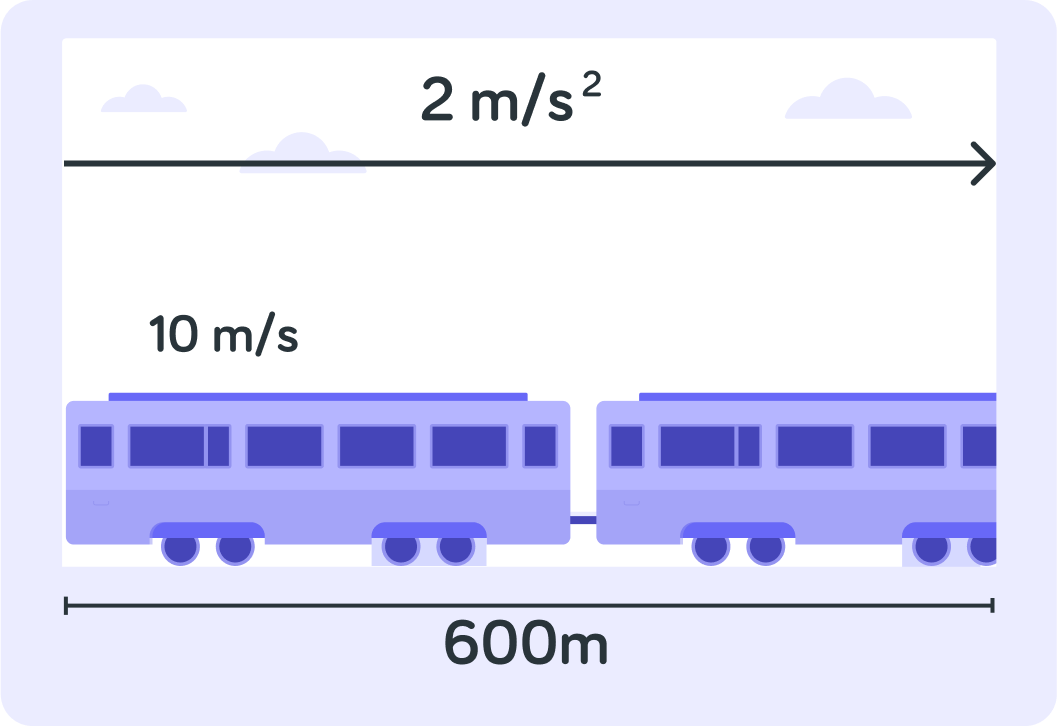
Use $v=\sqrt{u^2+2as}$ to work out this train's final velocity.

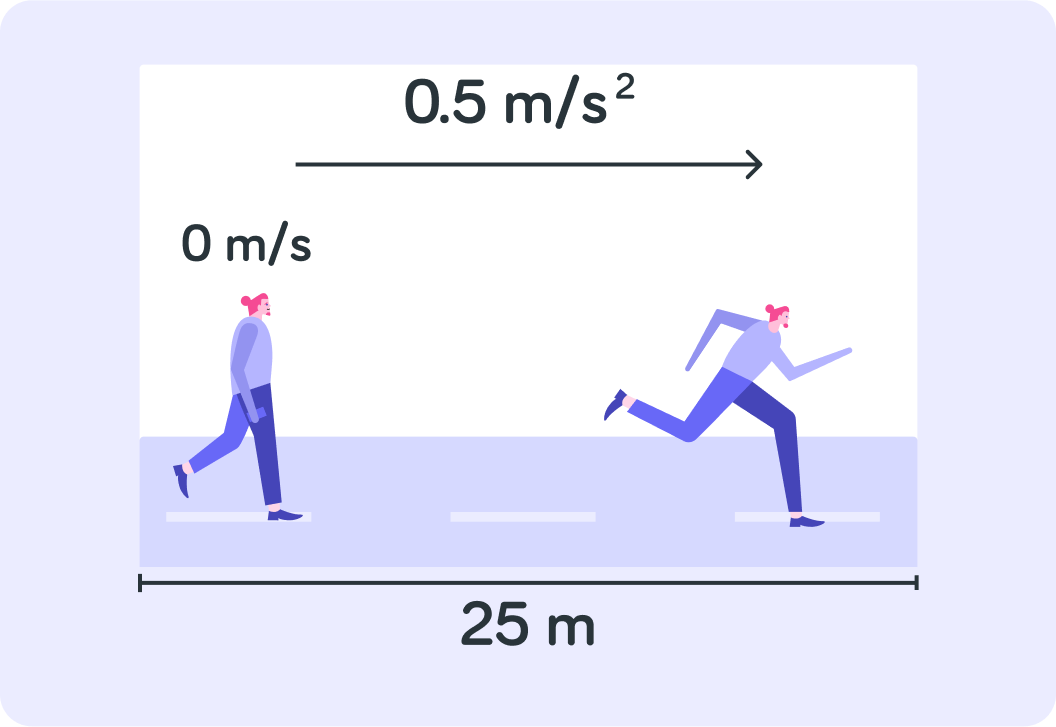
What is this person's final velocity?

A bowling ball is dropped from a height of $5m$ and accelerates uniformly due to gravity at $10\:m/s^2$ . It reaches a velocity of $10\:m/s$ right before it hits the ground. What was its initial velocity?

Summary!

An object that has uniform acceleration has constant change in velocity.

The equation $v^2-u^2=2as$ can only be used for uniformly accelerated motion.

To calculate acceleration, $a$ , we divide both sides by $2s$ to get...

$a=\frac{v^2-u^2}{2s}$

To calculate distance, $s$ , we divide both sides by $2a$ to get...

$s=\frac{v^2-u^2}{2a}$

To calculate the final velocity, $v$ we $+u^2$ to both sides and take the square-root to get...

$v=\sqrt{u^2 + 2as}$

To calculate the initial velocity, $u$ , we rearrange to get...

$u=\sqrt{v^2-2as}$